Regression mit studentisierten Daten
Bei einer einfachen linearen Regression versuchen wir zu vorgegebenen Datenpunkten \((x_1, y_1), \cdots (x_n, y_n)\) die Parameter einer möglichst passenden Gerade \(g(x)=\beta_0 + \beta_1 \cdot x\) zu schätzen.
Die Schätzung des y-Achsenabschnitts \(\hat\beta_0\) und der Steigung \(\hat\beta_1\) erfolgt dabei algebraisch exakt mittels:
\[\hat\beta_0 = \bar{y} - \hat\beta_1 \cdot \bar{x} \quad\text{und}\quad \hat\beta_1 = \frac{s_x}{s_y}\cdot r_{x,y}\]
Dabei sind \(\bar{x}\) bzw. \(\bar{y}\) die Mittelwerte und \(s_x\) bzw. \(s_y\) die Standardabweichungen der Datenpunkte \(x_i\) bzw. \(y_i\); darüberhinaus ist \(r_{x,y}\) der Korrelationskoeffizient der Datenpunkte.
Beim studentisieren werden die Datenpunkte bzgl. des Mittelwertes zentriert und bzgl der Standardabweichung normiert:
\[x_i^{\text{stud}} = \frac{x_i-\bar{x}}{s_x} \quad\text{bzw.}\quad y_i^{\text{stud}} = \frac{y_i-\bar{y}}{s_y}\]
Was passiert nun durch eine solche Studentisierung (oft auch z-Transformation genannt) mit den geschätzen Parametern?
Die Mittelwerte \(\bar{x}^{stud}\) und \(\bar{y}^{stud}\) werden zu Null. Die Standardabweichungen \(s_{x^{stud}}\) und \(s_{y^stud}\) werden zur Eins:
\[\bar{x}^{stud}=0=\bar{y}^{stud} \qquad s_{x^{stud}}= 1 = s_{y^{stud}}\]
Der y-Achsenabschnitt wird nun durch
\[\hat\beta_0^{stud} = \bar{y}^{stud} - \hat\beta_1^{stud} \cdot \bar{x}^{stud} = 0 - \hat\beta_1^{stud} \cdot 0 = 0\]
und die Steigung durch
\[ \hat\beta_1^{stud} = \frac{s_{x^{stud}}}{s_{y^{stud}}}\cdot r_{x^{stud},y^{stud}} = \frac{1}{1}\cdot r_{x^{stud},y^{stud}} = r_{x^{stud},y^{stud}} \]
geschätzt.
Für den Korrelationskoeffienten gilt nun \[ r_{x^{stud},y^{stud}} = \frac{s_{x^{stud},y^{stud}}}{s_{x^{stud}}\cdot_{y^{stud}}} = \frac{s_{x^{stud},y^{stud}}}{1 \cdot 1} = s_{x^{stud},y^{stud}}. \]
Damit Schätzen wir unsere Steigung \(\hat\beta_1^{stud}\) direkt aus der Kovarianz \(s_{x^{stud},y^{stud}}\).
Damit gilt:
\[\hat\beta_1^{stud} = r_{x^{stud},y^{stud}} = s_{x^{stud},y^{stud}} \in [-1, 1]\]
In Worten zusammengefasst: Im studentisierten Fall ist
- der y-Achsenabschnitt immer 0 und
- die Steigung immer ein Wert zwischen -1 und 1
Beispiel: mtcars- Daten
Auf Grundlage der Datentabelle mtcars wollen wir den linearer Zusammenhang zwischen dem Verbrauch (in Meilen pro Gallone mpg) und der Leistung (Pferdestärke hp) modellieren.1
library(mosaic)
# Wir nehmen die Datentabelle 'mtcars':
mtcars %>%
select(hp, mpg) -> dt
# Ein kurzer Blick aus die Daten:
df_stats( ~ hp + mpg, mean, sd, data = dt)
#> response mean sd
#> 1 hp 146.68750 68.562868
#> 2 mpg 20.09062 6.026948
# Wir vergleichen den Verbrauch (mpg, miles per gallon)
# mit den Pferdestärken (hp) mit Hilfe eines Streudiagramms.
# Dazu berechnen wir vorab die Mittelwerte
mean_hp <- mean(~ hp, data = dt)
mean_mpg <- mean(~ mpg, data = dt)
# und berechnen nun die Schätzwerte für die Regressionsgerade
beta_1 <- cov(mpg ~ hp, data = dt) / var(~ hp, data = dt)
beta_0 <- mean_mpg - beta_1 * mean_hp
# schliesslich zeichnen alles in das Streudiagramm ein:
gf_point(mpg ~ hp, data = dt) %>%
gf_hline(yintercept = ~ mean_mpg,
color = "grey60", linetype = "dashed") %>%
gf_vline(xintercept = ~ mean_hp,
color = "grey60", linetype = "dashed") %>%
gf_point(mean_mpg ~ mean_hp,
color = "red", size = 5, alpha = 0.2) %>%
gf_abline(slope = ~ beta_1, intercept = ~beta_0,
color = "dodgerblue") %>%
gf_lims(y = c(5,35))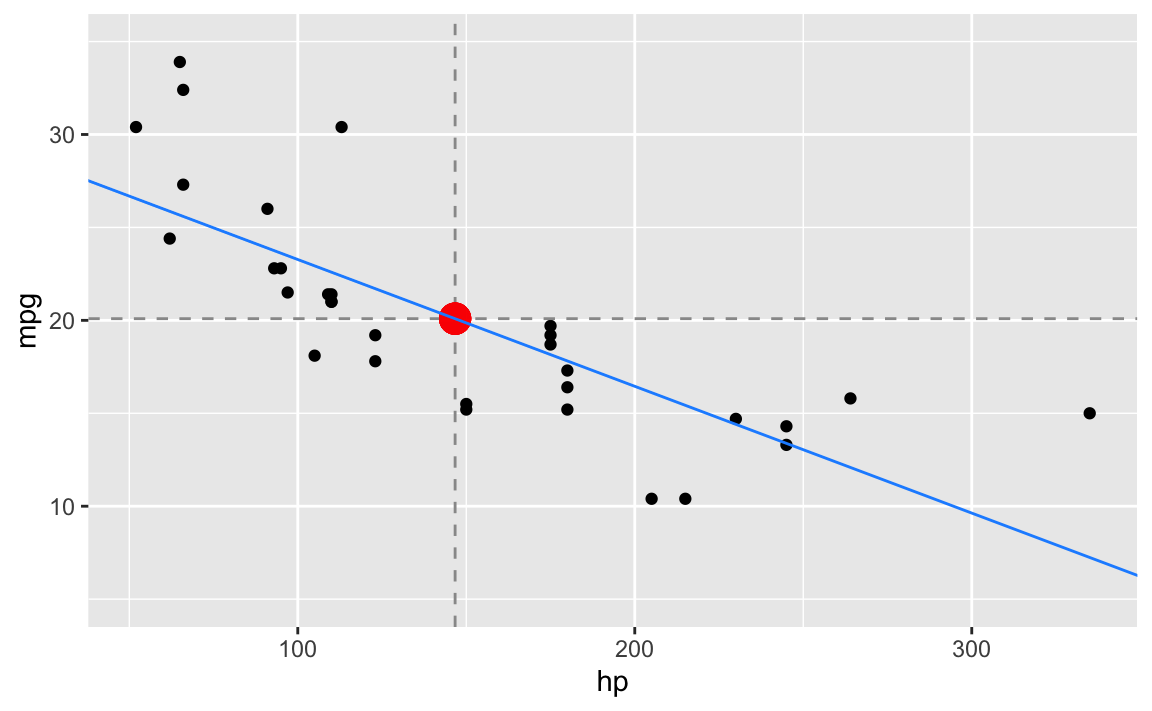
Die Funktionsvorschrift für die (blaue) Regressionsgerade lautet:
\[\begin{aligned} \hat{y} &= \hat\beta_0 + \hat\beta_1 \cdot x \\ &\approx 30.0988605 -0.0682283 \cdot x \\ &\approx 30.099 -0.068 \cdot x \end{aligned}\]
Studentisieren wir nun die mpg und hp Werte. In R können wir das mit der Funktion ‘zscore()’2 wie folgt machen:
dt %>%
mutate(
hp_stud = zscore(hp),
mpg_stud = zscore(mpg)
) -> dt
# Ein kurzer Blick aus die Daten:
df_stats( ~ hp_stud + mpg_stud, mean, sd, data = dt)
#> response mean sd
#> 1 hp_stud 1.040834e-17 1
#> 2 mpg_stud 7.112366e-17 1Der Grund für die kleinen Abweichungen von der Null bei den Mittelwerten sind unumgängliche Rundungsfehler, die der Computer macht!
# Wir "berechnen" die Mittelwerte:
mean_hp_stud <- 0 # = mean(~ hp_stud, data = dt)
mean_mpg_stud <- 0 # = mean(~ mpg_stud, data = dt)
# Berechnen wir nun die Schätzwerte für die Regressionsgerade:
beta_1_stud <- cov(mpg_stud ~ hp_stud, data = dt)
beta_0_stud <- 0 # = mean_mpg_stud - beta_1_stud * mean_hp_stud
# und zeichnen diese in unser Streudiagramm ein:
gf_point(mpg_stud ~ hp_stud, data = dt) %>%
gf_hline(yintercept = ~ mean_mpg_stud,
color = "grey60", linetype = "dashed") %>%
gf_vline(xintercept = ~ mean_hp_stud,
color = "grey60", linetype = "dashed") %>%
gf_point(mean_mpg_stud ~ mean_hp_stud,
color = "red", size = 5, alpha = 0.2) %>%
gf_abline(slope = ~ beta_1_stud, intercept = ~beta_0_stud,
color = "dodgerblue") %>%
gf_lims(y = c(-2,2))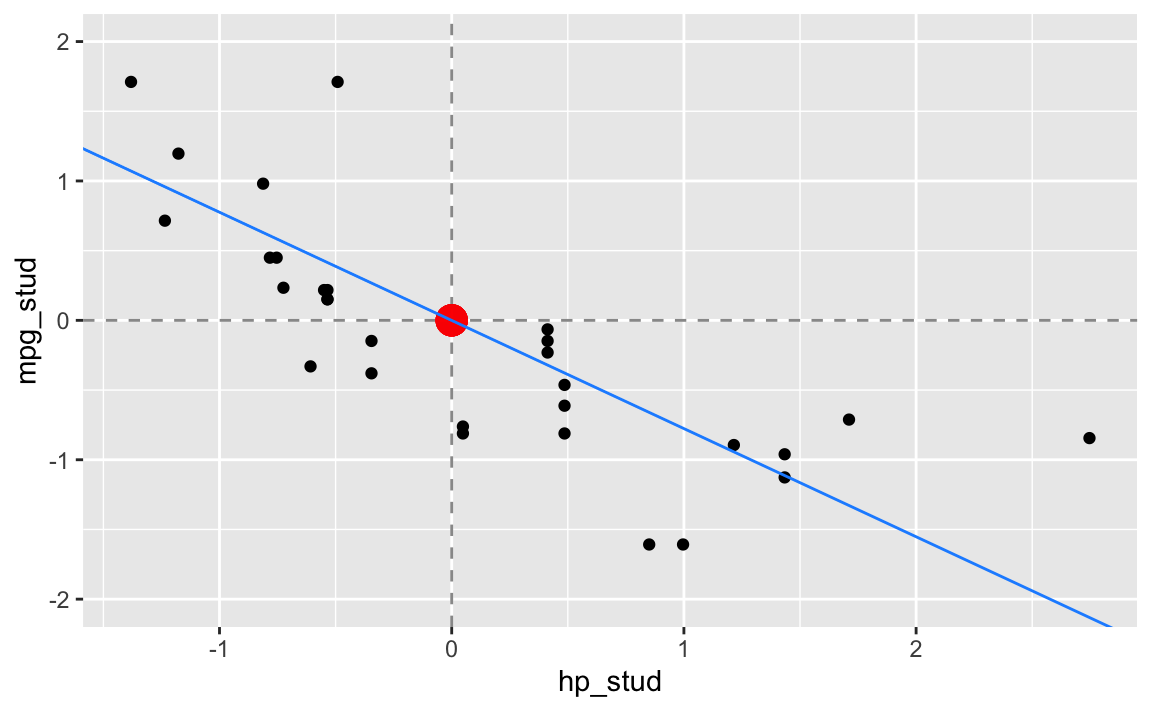
Die Regressionsgerade im studentisierten Problem lautet nun:
\[ \begin{aligned} \hat{y}^{stud} &= \hat\beta^{stud}_0 + \hat\beta_1^{stud} \cdot x^{stud} \\ &\approx 0 - 0.7761684 \cdot x^{stud} \\ &\approx 0 -0.776 \cdot x^{stud} \end{aligned} \]
Direkt mit ‘R’
Wir erhalten unsere Ergebnisse natürlich auch direkt in R, ohne selber die Werte auszurechnen:
# Ursprüngliches Modell:
erglm <- lm(mpg ~ hp, data = dt)
coef(erglm)
#> (Intercept) hp
#> 30.09886054 -0.06822828
# Studentisiertes Modell:
erglm_stud <- lm(mpg_stud ~ hp_stud, data = dt)
coef(erglm_stud)
#> (Intercept) hp_stud
#> -3.149357e-17 -7.761684e-01Zurückrechnen der studentisierten Werte in das ursprüngliche Problem
Aus dem Ergebnis des studentisierten Modells können wir die Koeffizenten des ursprünglichen Modells wie folgt berechnen:
\[\hat\beta_1 = \hat\beta_1^{stud} \cdot \frac{s_y}{s_x}\] und
\[\hat\beta_0 = \bar{y} - \hat\beta_1 \cdot \bar{x}\]
In R geht das wie folgt:
mean_mpg <- mean( ~ mpg, data = dt)
sd_mpg <- sd( ~ mpg, data = dt)
mean_hp <- mean( ~ hp, data = dt)
sd_hp <- sd( ~ hp, data = dt)
(beta_1 <- beta_1_stud * sd_mpg / sd_hp)
#> [1] -0.06822828
(beta_0 <- mean_mpg - beta_1 * mean_hp)
#> [1] 30.09886
### Fazit
...
## Reproduzierbarkeitsinformationen
#> R version 4.1.2 (2021-11-01) #> Platform: x86_64-apple-darwin17.0 (64-bit) #> Running under: macOS Catalina 10.15.7 #> #> Locale: de_DE.UTF-8 / de_DE.UTF-8 / de_DE.UTF-8 / C / de_DE.UTF-8 / de_DE.UTF-8 #> #> Package version: #> mosaic_1.8.3 tidyr_1.1.4 xfun_0.29 ```
Norman Markgraf
Diplom-Mathematiker
Norman Markgraf ist freiberuflicher Dozent für Mathematik, Statistik, Data Science und Informatik, sowie freiberuflicher Programmierer.