Über die Koeffizienten einer linearen Regression
Bei einer einfachen Regression versuchen wir zu gegebenen Datenpunkten \((x_1, y_1), ..., (x_n, y_n)\) eine möglichst passende Funktion \(g(x)\) zu finden, so dass \[y_i = g(x_i) + e_i\] gilt. Dabei tolerieren wir eine (kleine) Abweichung \(e_i\).
Bei einer einfachen linearen Regression gehen wir davon aus, dass die Datenpunkte (im wesentlichen) auf einer Geraden liegen. Mit \(g(x)=\beta_0 + \beta1 \cdot x\) ergibt sich dann für die Datenpunkte die Gleichung:
\[y_i = \beta_0 + \beta_1 \cdot x_i + e_i\]
Unsere Aufgabe besteht nun darin die Parameter \(\beta_0\) (y-Achsenabschnitt) und \(\beta_1\) (Steigung) an Hand der \(n\) Datenpunkte zu schätzen. Alle unsere Schätzungen kennzeichnen wir mit einem Dach (\(\hat{.}\)), um sie von den (in der Regel unbekannten) Parametern besser zu unterscheiden.
Wir suchen somit nach \(\hat\beta= \left(\hat\beta_0,\, \hat\beta_1\right)\), so dass die Gerade \(\hat\beta_0 + \hat\beta_1 \cdot x\) zu gegebenem \(x_i\) eine möglichst gute Schätzung von \(y_i\) (genannt \(\hat{y}_i\)) hat:
\[ \hat{y_i} = \hat\beta_0 + \hat\beta_1 \cdot x_i \]
Die Abweichung \(\hat{e_i}\) unserer Schätzung \(\hat{y}_i\) von dem gegebenen Wert \(y_i\) lässt sich schreiben als:
\[ \hat{e_i} = \hat{y_i} - y_i = \hat\beta_0 + \hat\beta_1 \cdot x_i - y_i \]
Wenn wir diese Abweichung über alle \(i\) minimieren, finden wir unser \(\hat\beta\).
Doch das wirft eine Frage auf: Wie genau messen wir die möglichst kleinste Abweichung der \(\hat{e_i}\) konkret?
Wir betrachten zunächst drei einfache Ideen:
Idee: Betrag der Summe der Abweichungen
Idee: Summe der absoluten Abweichungen
Idee: Summe der quadratischen Abweichungen
Gewöhnlich nutzen wir die quadratischen Abweichungen, weshalb wir die drei Ideen ebenso in umgekehrter Reihenfolge betrachten wollen:
3. Idee: Summe der quadratischen Abweichungen
Wir bezeichnen mit
\[\begin{aligned} QS &= QS(\hat\beta) = QS(\hat\beta_0, \hat\beta_1) \\ &= \sum\limits_{i=1}^n \hat{e_i}^2 = \sum\limits_{i=1}^n \left(\hat{y_i} - y_i \right)^2 \\ &= \sum\limits_{i=1}^n \left(\hat\beta_0 + \hat\beta_1 \cdot x_i - y_i \right)^2 \end{aligned}\]
die Quadrat-Summe der Abweichungen.
Gesucht wird \(\hat\beta=\left(\hat\beta_0,\,\hat\beta_1\right)\), so das \(QS\) minimiert wird.
Dies ist ein Minimierungsproblem, bei dem wir zu mindestens eine (exakte) mathematisch-algebraisch Lösung in Form eines stationären Punktes finden können. Dazu berechnen wir die Nullstelle der ersten partiellen Ableitung von \(QS\) nach \(\hat\beta_0\) bzw. \(\hat\beta_1\).
Vorbemerkungen
Wegen \(\bar{x} = \frac{1}{n} \sum\limits_{i=1}^n x_i\) ist \(n \cdot \bar{x} =\sum\limits_{i=1}^n x_i\) und analog \(n \cdot \bar{y} =\sum\limits_{i=1}^n y_i\)
Schätzen des y-Achenabschnitts \(\hat\beta_0\)
Es ist:
\[\begin{aligned} \frac{\partial}{\partial \hat\beta_0} \, QS &= 2 \cdot \sum\limits_{i=1}^n \left(\hat\beta_0 + \hat\beta_1 \cdot x_i - y_i \right) \cdot 1 \\ &= 2 \cdot \left(\sum\limits_{i=1}^n \hat\beta_0 + \sum\limits_{i=1}^n\hat\beta_1 \cdot x_i - \sum\limits_{i=1}^n y_i\right) \\ &= 2 \cdot \left( n \cdot \hat\beta_0 + \hat\beta_1\cdot\sum\limits_{i=1}^n x_i - \sum\limits_{i=1}^n y_i \right) \\ &= 2 \cdot \left( n \cdot \hat\beta_0 + \hat\beta_1\cdot n \cdot \bar{x} - n \cdot\bar{y} \right) \\ &= 2 \cdot n \cdot \left( \hat\beta_0 + \hat\beta_1\cdot \bar{x} -\bar{y} \right) \end{aligned}\]
Um stationäre Punkte zu ermitteln, müssen wir den Ausdruck nun gleich Null setzen und erhalten:
\[\begin{aligned} 0 &= \frac{\partial}{\partial \hat\beta_0} \, QS \\ &= 2 \cdot n \cdot \left( \hat\beta_0 + \hat\beta_1\cdot \bar{x} -\bar{y} \right) \qquad | : (2 \cdot n) \\ &= \hat\beta_0 + \hat\beta_1\cdot \bar{x} -\bar{y} \end{aligned}\]
Stellen wir nach \(\hat\beta_0\) um, erhalten wir:
\[\begin{aligned} \hat\beta_0 &= - \hat\beta_1\cdot\bar{x} + \bar{y} \\ \hat\beta_0 &= \bar{y} - \hat\beta_1\cdot\bar{x} \end{aligned}\]
Um \(\hat\beta_0\) zu bestimmen, benötigen wir \(\hat\beta_1\).
Schätzen der Steigung \(\hat\beta_1\)
Es ist:
\[\begin{aligned} \frac{\partial}{\partial \hat\beta_1} \, QS &= 2 \cdot \sum\limits_{i=1}^n \left(\hat\beta_0 + \hat\beta_1 \cdot x_i - y_i \right) \cdot x_i \\ &= 2 \cdot \left(\sum\limits_{i=1}^n \hat\beta_0 \cdot x_i + \sum\limits_{i=1}^n \hat\beta_1 \cdot x_i\cdot x_i- \sum\limits_{i=1}^n y_i \cdot x_i\right) \\ &= 2 \cdot \left(\hat\beta_0 \cdot \sum\limits_{i=1}^n x_i + \hat\beta_1 \cdot\sum\limits_{i=1}^n x_i^2- \sum\limits_{i=1}^n y_i \cdot x_i\right) \\ &= 2 \cdot \left(\hat\beta_0 \cdot n \cdot \bar{x} + \hat\beta_1 \cdot\sum\limits_{i=1}^n x_i^2- \sum\limits_{i=1}^n y_i \cdot x_i\right) \end{aligned}\]
Wir ersetzen nun \(\hat\beta_0\) durch \(\bar{y} - \hat\beta_1\cdot \bar{x}\) und erhalten:
\[\begin{aligned} \frac{\partial}{\partial \hat\beta_1} \, QS &= 2 \cdot \left(\hat\beta_0 \cdot n \cdot \bar{x} + \hat\beta_1 \cdot\sum\limits_{i=1}^n x_i^2- \sum\limits_{i=1}^n y_i \cdot x_i\right) \\ &= 2 \cdot \left(\left(\bar{y} - \hat\beta_1\cdot \bar{x}\right) \cdot n \cdot \bar{x} + \hat\beta_1 \cdot\sum\limits_{i=1}^n x_i^2- \sum\limits_{i=1}^n y_i \cdot x_i\right) \\ &= 2 \cdot \left(n \cdot\bar{y} \cdot \bar{x} - n \cdot \hat\beta_1 \cdot \bar{x}^2 + \hat\beta_1 \cdot\sum\limits_{i=1}^n x_i^2- \sum\limits_{i=1}^n y_i \cdot x_i\right) \\ &= 2 \cdot \left(n \cdot\bar{y} \cdot \bar{x} - \sum\limits_{i=1}^n y_i \cdot x_i + \hat\beta_1 \cdot \left(\sum\limits_{i=1}^n x_i^2- n \cdot \bar{x}^2\right)\right) \\ \end{aligned}\]
Mit Hilfe des Verschiebesatzes von Steiner (zweimal angewendet) erhalten wir:
\[\begin{aligned} \frac{\partial}{\partial \hat\beta_1} \, QS &=2 \cdot \left(n \cdot\bar{y} \cdot \bar{x} - \sum\limits_{i=1}^n y_i \cdot x_i + \hat\beta_1 \cdot \left(\sum\limits_{i=1}^n x_i^2- n \cdot \bar{x}^2\right)\right) \\ &=2 \cdot \left(- \left(\sum\limits_{i=1}^n y_i \cdot x_i - n \cdot \bar{y} \cdot \bar{x} \right)+ \hat\beta_1 \cdot \left(\sum\limits_{i=1}^n x_i^2- n \cdot \bar{x}^2\right)\right) \\ &=2 \cdot \left(\hat\beta_1 \cdot \left(\sum\limits_{i=1}^n x_i^2- n \cdot \bar{x}^2\right)- \left(\sum\limits_{i=1}^n y_i \cdot x_i - n \cdot \bar{y} \cdot \bar{x} \right)\right) \\ &= 2 \cdot \left(\hat\beta_1 \cdot \sum\limits_{i=1}^n(x_i-\bar{x})^2 - \sum\limits_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y})\right) \end{aligned}\]
Wir setzen nun wieder den Ausdruck gleich Null:
\[\begin{aligned} 0 &= 2 \cdot \left(\hat\beta_1 \cdot \sum\limits_{i=1}^n(x_i-\bar{x})^2 - \sum\limits_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y})\right) \qquad | : 2\\ &= \hat\beta_1 \cdot \sum\limits_{i=1}^n(x_i-\bar{x})^2 - \sum\limits_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y}) \end{aligned}\]
Und stellen dann nach \(\hat\beta_1\) um:
\[\begin{aligned} \hat\beta_1 \cdot \sum\limits_{i=1}^n(x_i-\bar{x})^2 &= \sum\limits_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y}) \\ \hat\beta_1 &= \frac{\sum\limits_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y})}{\sum\limits_{i=1}^n(x_i-\bar{x})^2} \end{aligned}\]
Wir können nun Zähler und Nenner der rechten Seite mit \(\frac{1}{n}\) erweitern und erhalten so:
\[\begin{aligned} \hat\beta_1 &= \frac{\frac{1}{n} \cdot\sum\limits_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y})}{\frac{1}{n} \cdot\sum\limits_{i=1}^n (x_i-\bar{x})^2} \\ &= \frac{\sigma_{x,y}}{\sigma^2_x} \\ \end{aligned}\]
Oder aber wir erweitern mit \(\frac{1}{n-1}\) und erhalten:
\[\begin{aligned} \hat\beta_1 &= \frac{\frac{1}{n-1} \cdot\sum\limits_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y})}{\frac{1}{n-1} \cdot\sum\limits_{i=1}^n (x_i-\bar{x})^2} \\ &= \frac{s_{x,y}}{s^2_{x}} \end{aligned}\]
Damit können wir zur Berechnung sowohl die Kovarianz der Grundgesamtheit \(\sigma_{x,y}\) und die Varianz \(\sigma^2_x\) von \(x\), als auch deren Schätzer \(s_{x,y}\) und \(s^2_x\) verwendet werden!
Diese Methode nennt sich Methode der kleinsten Quadrate (engl. ordenary least square method) und wir sprechen dann auch von den Kleinste-Quadrate-Schätzern (oder kurz KQ-Schätzer bzw. OLS-Schätzer) \(\hat\beta_0\) und \(\hat\beta_1\).
Erweitern wir den Ausdruck mit Standardabweichung \(\sigma_y\) bzw. \(s_y\), so erhalten wir:
\[\begin{aligned} \hat\beta_1 &= \frac{\sigma_{x,y}}{\sigma^2_x} \cdot \frac{\sigma_y}{\sigma_y} = \frac{\sigma_{x,y}}{\sigma_x \cdot \sigma_x} \cdot \frac{\sigma_y}{\sigma_y} = \frac{\sigma_{x,y}}{\sigma_x \cdot \sigma_y} \cdot \frac{\sigma_y}{\sigma_x} \\ &= \rho_{x,y} \cdot \frac{\sigma_y}{\sigma_x} \\ \end{aligned}\]
und analog für die Schätzer:
\[\begin{aligned} \hat\beta_1 &= \frac{s_{x,y}}{s^2_x} \cdot \frac{s_y}{s_y} = \frac{s_{x,y}}{s_x \cdot s_x} \cdot \frac{s_y}{s_y} = \frac{s_{x,y}}{s_x \cdot s_y} \cdot \frac{s_y}{s_x} \\ &= r_{x,y} \cdot \frac{s_y}{s_x} \\ \end{aligned}\]
Die Steigung \(\hat\beta_1\) hat somit eine direkte Beziehung mit dem Korrelationskoeffizenten \(\rho\) (der Grundgesamtheit) bzw. \(r\) (der Stichprobe).
Für eine Berechnung in R heißt dies: wir können die Regressionskoeffizienten \(\hat\beta_0\) und \(\hat\beta_1\) direkt algebraisch ausrechnen, wenn wir
die Standardabweichungen von \(x\) und \(y\) und den Korrelationskoeffizienten oder
die Varianz von \(x\) und Kovarianz von \(x\) und \(y\)
haben.
Ein Beispiel in R:
Auf Grundlage der Datentabelle mtcars wollen wir Prüfen wie ein linearer Zusammenhang zwischen dem Verbrauch (in Meilen pro Gallone mpg) und der Leistung (Pferdestärke hp) modelliert werden kann.1
library(mosaic)
# Wir nehmen die Datentabelle 'mtcars':
mtcars %>%
select(hp, mpg) -> dt
# Ein kurzer Blick auf die Daten:
favstats(~ hp, data=dt)[c("mean","sd")]
#> mean sd
#> 146.6875 68.56287
favstats(~ mpg, data=dt)[c("mean","sd")]
#> mean sd
#> 20.09062 6.026948
# Wir vergleichen den Verbrauch (mpg, miles per gallon)
# mit den Pferdestärken (hp) mit Hilfe eines Streudiagramms:
gf_point(mpg ~ hp, data = dt) %>%
gf_lims(y = c(5,35))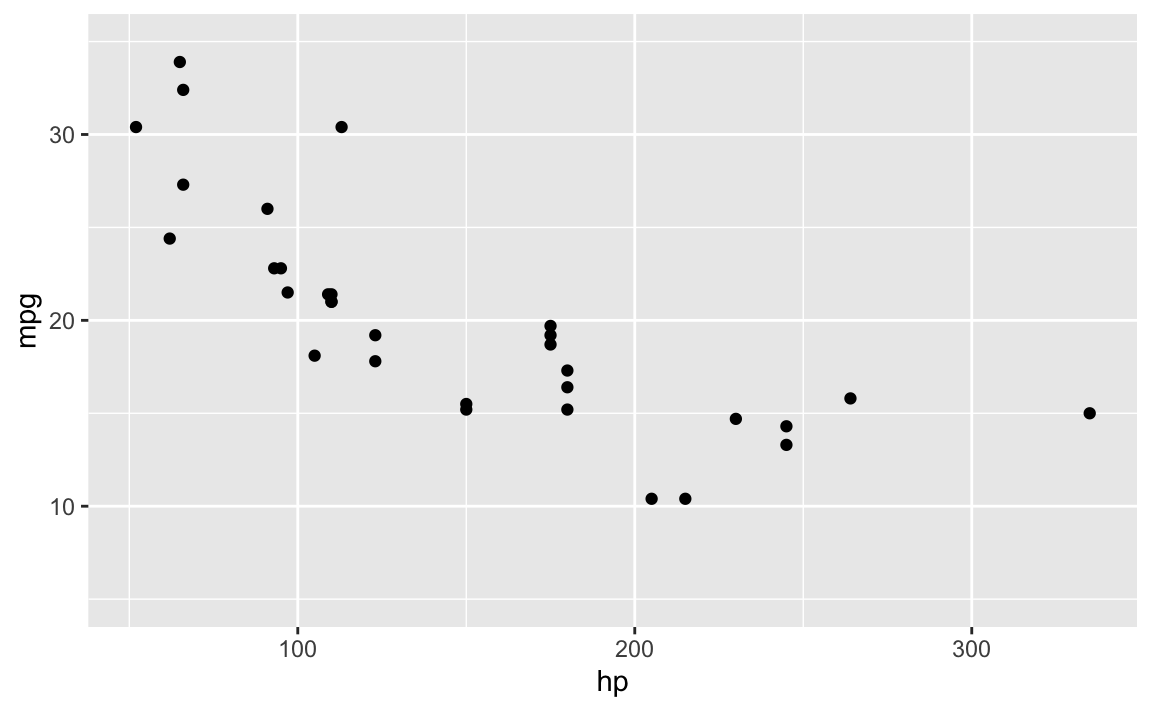
Berechnen wir zunächst die Mittelwerte von \(x\) (also ‘hp’) und \(y\) (also ‘mpg’)
(mean_hp <- mean(~ hp, data = dt))
#> [1] 146.6875
(mean_mpg <- mean(~ mpg, data = dt))
#> [1] 20.09062und zeichnen die Punkt \((\bar{x}, \bar{y}) = (146.69, 20.09)\) in unser Streudiagramm ein:
gf_point(mpg ~ hp, data = dt) %>%
gf_hline(yintercept = ~ mean_mpg, color = "grey60", linetype = "dashed") %>%
gf_vline(xintercept = ~ mean_hp, color = "grey60", linetype = "dashed") %>%
gf_point(mean_mpg ~ mean_hp, color = "red", size = 5, alpha = 0.2) %>%
gf_lims(y = c(5,35))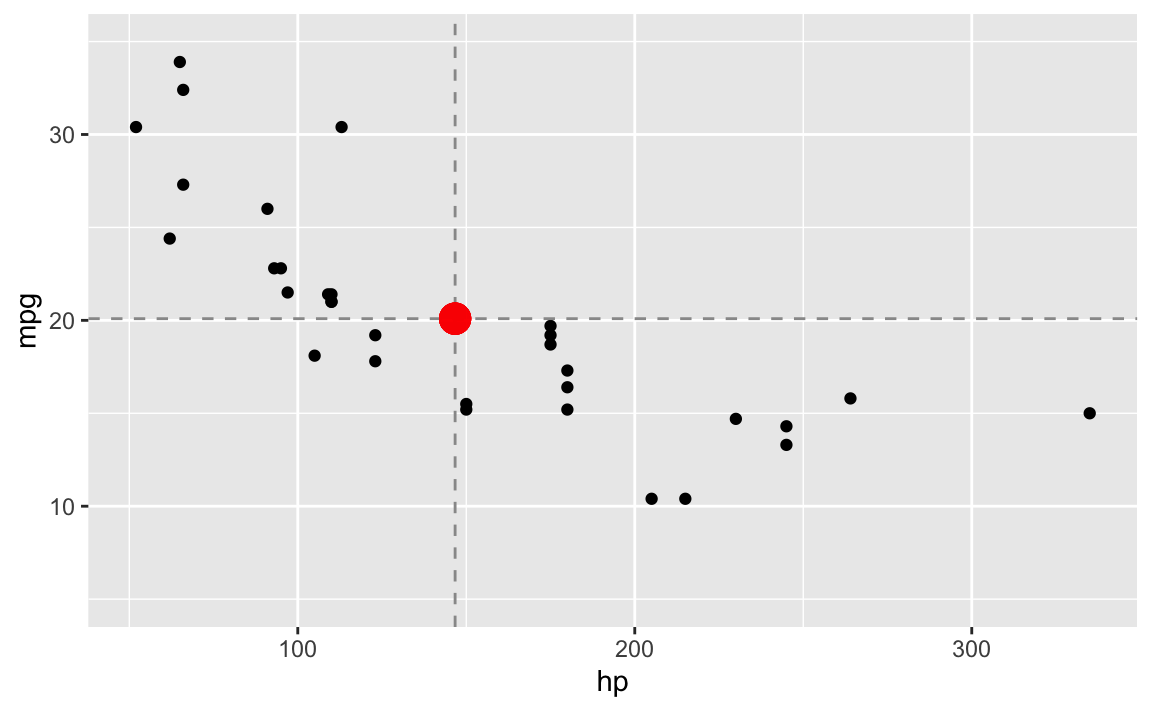
Berechnen wir nun die Schätzwerte für die Regressionsgerade
(beta_1 <- cov(mpg ~ hp, data = dt) / var(~ hp, data = dt))
#> [1] -0.06822828
(beta_0 <- mean_mpg - beta_1 * mean_hp)
#> [1] 30.09886und zeichnen diese in unser Streudiagramm ein:
gf_point(mpg ~ hp, data = dt) %>%
gf_hline(yintercept = ~ mean_mpg, color = "grey60", linetype = "dashed") %>%
gf_vline(xintercept = ~ mean_hp, color = "grey60", linetype = "dashed") %>%
gf_point(mean_mpg ~ mean_hp, color = "red", size = 5, alpha = 0.2) %>%
gf_abline(slope = ~ beta_1, intercept = ~beta_0, color = "dodgerblue") %>%
gf_lims(y = c(5,35))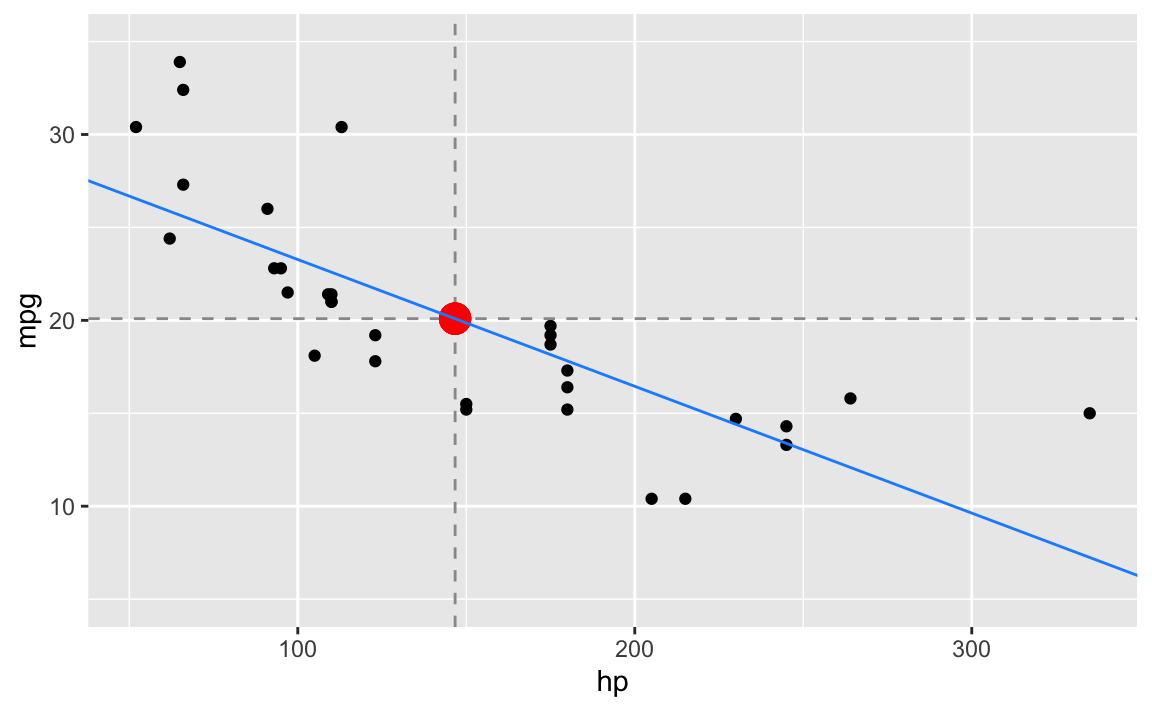
Die Funktionsvorschrift für die (blaue) Regressionsgerade lautet:
\[\begin{aligned} \hat{y} &= \hat\beta_0 + \hat\beta_1 \cdot x \\ &\approx 30.0988605 -0.0682283 \cdot x \\ &\approx 30.099 -0.068 \cdot x \end{aligned}\]
Studentisieren – einmal hin und einmal zurück
Was passiert eigentlich, wenn wir unsere \(x\) und \(y\) Werte studentisieren (aka standardisieren oder z-transformieren)?
Zur Erinnerung, studentisieren geht so: \[x^{stud} = \frac{x - \bar{x}}{s_x}\]
In R können wir das mit der Funktion ‘zscore’ wie folgt machen:
dt %>%
mutate(
hp_stud = zscore(hp),
mpg_stud = zscore(mpg)
) -> dtNatürlich sind die Mittelwerte nun Null und die Standardabweichungen Eins:
favstats(~ hp_stud, data=dt)[c("mean","sd")]
#> mean sd
#> 1.040834e-17 1
favstats(~ mpg_stud, data=dt)[c("mean","sd")]
#> mean sd
#> 7.112366e-17 1Der Grund für die kleinen Abweichungen von der Null bei den Mittelwerten sind unumgängliche Rundungsfehler, die der Computer macht!
Schauen wir uns nun das Streudiagramm an, zusammen mit dem Mittelpunkt \((0,0)\)
gf_point(mpg_stud ~ hp_stud, data = dt) %>%
gf_point(0 ~ 0, color = "red", size = 5, alpha = 0.2) %>%
gf_lims(y = c(-2, 2))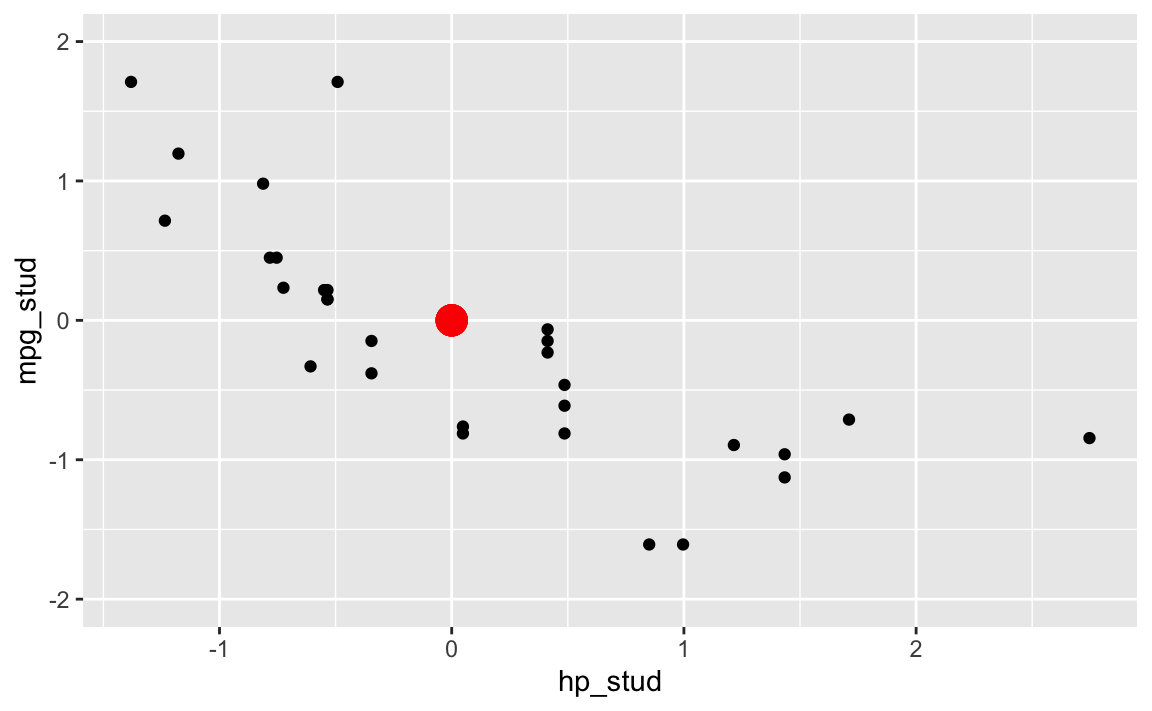 Auch wenn die Skalierungen sich geändert haben, die Diagramme sind sehr ähnlich.
Auch wenn die Skalierungen sich geändert haben, die Diagramme sind sehr ähnlich.
Bestimmen wir die Koeffizienten der Regressionsgerade
(beta_stud_1 <- cov(mpg_stud ~ hp_stud, data = dt))
#> [1] -0.7761684
(beta_stud_0 <- 0 - beta_stud_1 * 0)
#> [1] 0und setzen sie in das Streudiagramm ein:
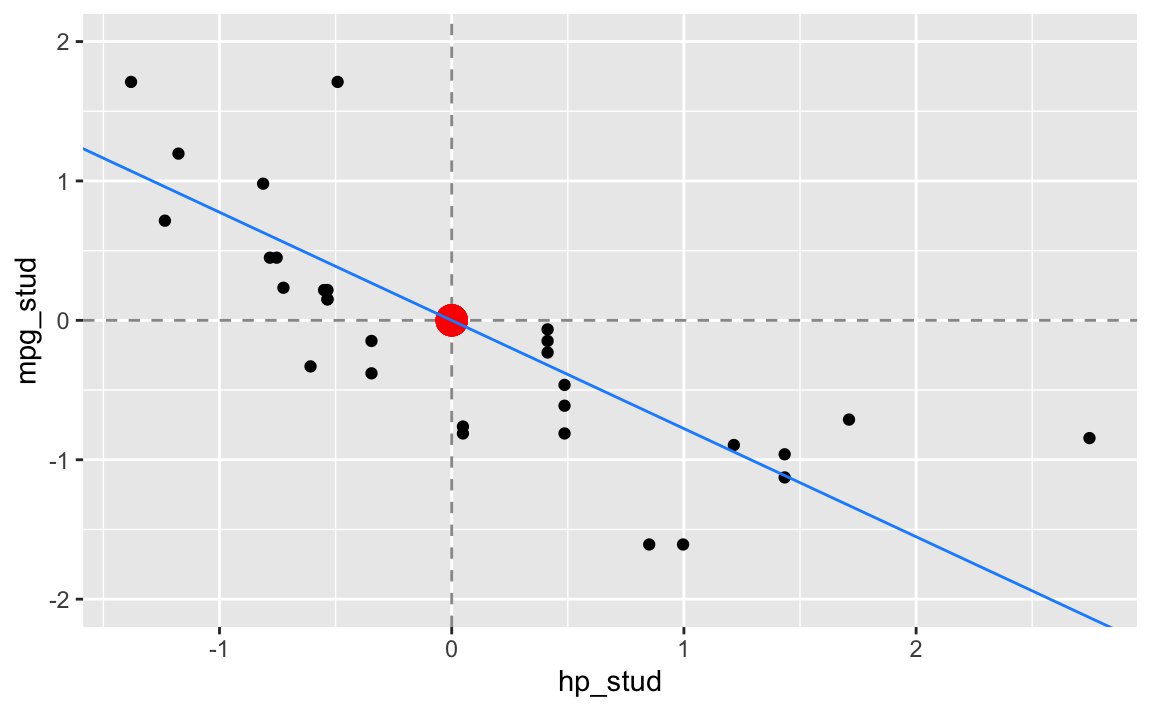
Wir können das studentisierte Problem auch wieder auf unser ursprüngliches zurück rechnen.
Die Regressionsgerade im studentisierten Problem lautet:
\[\begin{aligned} \hat{y}^{stud} &= \hat\beta^{stud}_0 + \hat\beta_1^{stud} \cdot x^{stud} \\ &\approx 0 -0.7761684 \cdot x^{stud} \\ &\approx 0 -0.776 \cdot x^{stud} \end{aligned}\]
Rechnen wir nun mittels der Formel \[\hat\beta_1 = \hat\beta_1^{stud} \cdot \frac{s_y}{s_x}\]
die Steigung um, so erhalten wir:
(b1 <- beta_stud_1 * sd(dt$mpg) / sd(dt$hp))
#> [1] -0.06822828Und setzen wir das in unsere Gleichung zur Bestimmung von \(\hat\beta_0\) ein:
(b0 <- mean(dt$mpg) - b1 * mean(dt$hp))
#> [1] 30.09886so erhalten wir die Schätzwerte des ursprünglichen Problem.
Ein anderer Weg um die Regressionskoeffizenten zu bestimmen…
Gehen wir das Problem noch einmal neu an. Wir suchen \(\hat\beta=(\hat\beta_0, \hat\beta_1)\) welches \(QS(\hat\beta) = QS(\hat\beta_0, \hat\beta_1) = \sum\limits_{i=1}^n \left(\hat\beta_0 + \hat\beta_1 \cdot x_i - y_i \right)^2\) minimiert.
Statt es direkt, wie oben durch Null setzen der partiellen Ableitungen, zu bestimmen, wählen wir nun einen mathematisch-numerischen Ansatz und wollen \(\hat\beta \in \mathbf{R}^2\) als Optimierungsproblem mit Hilfe des Gradientenverfahrens lösen.
Beim Gradientenverfahren wird versucht, ausgehend von einem Startwert \(\hat\beta^0 \in \mathbf{R}^2\), gemäß der Iterationsvorschrift
\[ \hat\beta^{k+1} = \hat\beta^{k} + \alpha^k \cdot d^k \]
für alle \(k=0,1, ...\) eine Näherungslösung für \(\hat\beta\) zu finden. Dabei ist \(\alpha^k > 0\) eine positive Schrittweite und \(d^k\in\mathbf{R}^n\) eine Abstiegsrichtung, welche wir in jedem Iterationsschritt \(k\) so bestimmen, dass die Folge \(\hat\beta^k\) zu einem stationären Punkt, unserer Näherungslösung, konvergiert.
Im einfachsten Fall, dem Verfahren des steilsten Abstieges, wird der Abstiegsvektor \(d^k\) aus dem Gradienten \(\nabla QS\) wie folgt bestimmt:
\[d^k = -\nabla QS\left(\hat\beta^k\right)\]
Wegen \[ \frac{\partial}{\partial \hat\beta_0} \, QS = 2 \cdot n \cdot \left( \hat\beta_0 + \hat\beta_1\cdot\bar{x} - \bar{y} \right) \]
und
\[ \frac{\partial}{\partial \hat\beta_1} \, QS = 2 \cdot \left(\hat\beta_1 \cdot \sum\limits_{i=1}^n(x_i-\bar{x})^2 - \sum\limits_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y}) \right) \]
gilt:
\[\begin{aligned} \nabla QS(\hat\beta) &= \nabla QS(\hat\beta_0, \hat\beta_1) \\ &= 2 \cdot \begin{pmatrix} n \cdot(\hat\beta_0 + \hat\beta_1\cdot\bar{x} - \bar{y}) \\ \hat\beta_1 \cdot \sum\limits_{i=1}^n(x_i-\bar{x})^2 - \sum\limits_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y}) \end{pmatrix} \end{aligned}\]
Wir wollen hier von Anfang an mit den studentisierten Werten arbeiten, weil diese numerisch viele Vorteile haben. Darum vereinfachen sich die beiden partiellen Ableitungen noch einmal zu:
\[ \frac{\partial}{\partial \hat\beta_0} \, QS = 2 \cdot v \]
und
\[\begin{aligned} \frac{\partial}{\partial \hat\beta_1} \, QS &= 2 \cdot \left(\hat\beta_1 \cdot \sum\limits_{i=1}^n(x_i-\bar{x})^2 - \sum\limits_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y})\right) \\ &= 2 \cdot (n-1) \left(\hat\beta_1 \cdot s^2_{x} - s_{x,y}\right) \end{aligned}\]
Somit gilt:
\[\begin{aligned} \nabla QS(\hat\beta) &= \nabla QS(\hat\beta_0, \hat\beta_1) \\ &= 2 \cdot \begin{pmatrix} n \cdot \hat\beta_0 \\ (n-1) \left(\hat\beta_1 \cdot s^2_{x} - s_{x,y}\right) \end{pmatrix} \end{aligned}\]
Um die Varianz und die Kovarianz nicht jedesmal neu zu berechnen, speichern wir die Ergebnisse vorab. Ebenso, damit der Quellcode kürzer wird, speichern wir in \(x\) und \(y\) die studentisierten Werte von \(hp\) und \(mpg\):
# Vorbereitungen
var_x <- var(~ hp_stud, data = dt)
cov_xy <- cov(mpg_stud ~ hp_stud, data = dt)
n <- length(dt$hp_stud)
x <- dt$hp_stud
y <- dt$mpg_studNun erstellen wir die \(QS\) und \(\nabla QS\) Funktionen: Wir definieren diese Funktion wie folgt in R:
qs <- function(b_0, b_1) {
sum((b_1 * x - y)**2)
}
nabla_qs <- function(b_0, b_1) {
c(2 * n * b_0,
2 * (n - 1) * (b_1 * var_x - cov_xy)
)
}Die Schrittweite \(alpha\) bestimmen wir mit Hilfe der Armijo-Bedingung und der Backtracking Liniensuche: Diese formalisiert das Konzept “genügend” in der geforderten Verringerung des Funktionswertes. Die Bedingung \(f(x^k + \alpha d^k) < f(x^k)\) wird modifiziert zu \[f(x^k + \alpha d^k) \leq f(x^k) + \sigma \alpha \left(\nabla f(x^k)\right)^T d^k,\] mit \(\sigma\in (0,1)\). Die Armijo-Bedingung umgeht Konvergenzprobleme der einfachen Bedingung, indem sie fordert, dass die Verringerung zumindest proportional zur Schrittweite und zur Richtungsableitung \(\left(\nabla f(x^k)\right)^T d^k\) ist, mit Hilfe der Proportionalitätskonstante \(\sigma\). In der Praxis werden oft sehr kleine Werte verwendet, z.B. \(\sigma=0.0001\).
Die Backtracking-Liniensuche verringert die Schrittweite wiederholt um den
Faktor \(\rho\) (rho) , bis die Armijo-Bedingung erfüllt ist.
Sie terminiert garantiert nach einer endlichen Anzahl von Schritten. Weshalb wir
sie hier einsetzen:
alpha_k <- function(b_0, b_1, d_k, alpha = 1, sigma = 0.0001, rho = 0.5) {
d_0 <- d_k[1]
d_1 <- d_k[2]
nabla <- nabla_qs(b_0, b_1)
n_0 <- nabla[1]
n_1 <- nabla[2]
lhs <- qs(b_0 + alpha*d_0, b_1 + alpha*d_1)
rhs <- qs(b_0, b_1) + sigma*alpha*(n_0*d_0 + n_1*d_1)
while (lhs > rhs) {
alpha <- rho * alpha
lhs <- qs(b_0 + alpha*d_0, b_1 + alpha*d_1)
rhs <- qs(b_0, b_1) + sigma*alpha*(n_0*d_0 + n_1*d_1)
}
return(alpha)
}Ein paar Einstellungen vorab:
# maximale Anzahl an Iterationen
max_iter <- 1000
iter <- 0
# Genauigkeit
eps <- 10**-6
# Startwerte
b_0 <- 0
b_1 <- -1 Für eine vorgegebene Genauigkeit \(eps=10^{-6}\), den Startwerten \(\hat\beta_0^0 = 0\) und \(\hat\beta_1^0 = -1\) können wir somit das Verfahren starten:
while (TRUE) {
iter <- iter + 1
d_k <- -nabla_qs(b_0, b_1)
ad_ <- alpha_k(b_0, b_1, d_k) * d_k
x0 <- b_0 + ad_[1]
x1 <- b_1 + ad_[2]
if ((abs(b_0 - x0) < eps) & (abs(b_1 - x1) < eps) | (iter > max_iter)) {
break
}
b_0 <- x0
b_1 <- x1
}Wir haben in \(203\) Iterationsschritten das folgende Ergebnis für die Regressionskoeffizienten:
\[\hat\beta_0^{stud} = 0 \qquad \hat\beta_1^{stud} = -0.7761689\]
Betrachten wir die daraus erstellte Regressionsgerade:
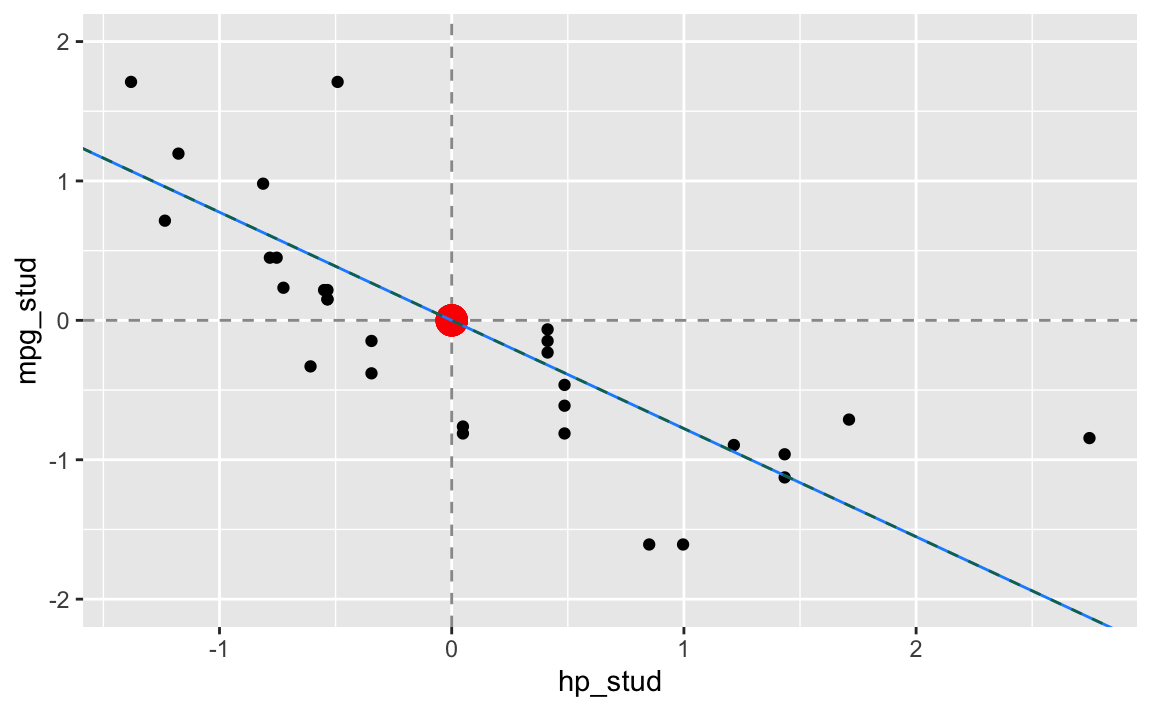
Um die Regressionskoeffizienten für unser ursprüngliches Problem zu erhalten müssen wir wie folgt zurück rechnen:
(b1 <- b_1 * sd(dt$mpg) / sd(dt$hp))
#> [1] -0.06822832
(b0 <- mean(dt$mpg) - b1 * mean(dt$hp))
#> [1] 30.09887Die Geradengleichung für das ursprüngliches Problem lautet somit:
\[\begin{aligned} \hat{y} &= \hat\beta_0 + \hat\beta_1 \cdot x \\ &\approx 30.0988668 -0.0682283 \cdot x \\ &\approx 30.099 -0.068 \cdot x \end{aligned}\]
Die R Funktion optim
In R gibt es bessere Optimierungsmethoden, als die hier verwendete.
Zum Beispiel können wir die Funktion optim verwenden.
Die Funktion optim benötigt die zu optimierende \(f(x)\) und
ggf. die Gradientenfunktion \(gf(x)\) sowie einen Startpunkt \(x^0\):
f <- function(beta) {
qs(beta[1], beta[2])
}
grf <- function(beta) {
nabla_qs(beta[1], beta[2])
}
# Der eigentliche Aufruf von optim:
ergb <- optim(c(0,-0.5),f ,grf, method = "CG")
# Auslesen der Schätzer aus dem Ergebnis:
(optim_beta_0 <- ergb$par[1])
#> [1] 0
(optim_beta_1 <- ergb$par[2])
#> [1] -0.7761683Wir erhalten somit für das studentisierte Problem die Gerade:
\[\begin{aligned} \hat{y}^{stud} &= \hat\beta_0^{stud} + \hat\beta_1^{stud} \cdot x^{stud} \\ &\approx 0 -0.7761683 \cdot x^{stud} \\ &\approx 0 -0.776 \cdot x^{stud} \end{aligned}\]
Für das ursprüngliche Problem rechnen wir mittels
optim_b1 <- optim_beta_1 * sd(dt$mpg) / sd(dt$hp)
optim_b0 <- mean(dt$mpg) - optim_b1 * mean(dt$hp)um und erhalten:
\[\begin{aligned} \hat{y} &= \hat\beta_0 + \hat\beta_1 \cdot x \\ &\approx 30.0988601 -0.0682283 \cdot x \\ &\approx 30.099 -0.068 \cdot x \end{aligned}\]
2. Idee: Summe der absoluten Abweichungen
Wir ändern nun die Abweichungsmessfunktion von der Quadrat-Summe hin zu den Absolut-Summen:
\[AS = AS(\hat\beta) = AS(\hat\beta_0, \hat\beta_1) = \sum_{i=1}^n |\hat{y}_i - y_i|\]
Auch hier wollen wir mit den studentisierten Daten arbeiten und stellen die Funktion der Absolut-Summen auf:
# Absolute Abweichungssummen
as <- function(b_0, b_1) {
return(sum(abs(b_0 + b_1 * x - y)))
}Danach konstruieren wir die zu optimierende Funktion \(f\):
# Zu optimierende Funktion
f <- function(beta) {
as(beta[1], beta[2])
}Diesmal nutzen wir optim ohne eine Gradientenfunktion:
ergb <- optim(c(0,-1), f)
# Schätzer auslesen
(opti_as_beta_0 <- ergb$par[1])
#> [1] -0.1304518
(opti_as_beta_1 <- ergb$par[2])
#> [1] -0.6844911Schauen wir uns nun die so erhaltene Gerade im Vergleich mit der ‘normalen’ Regressionsgerade an:
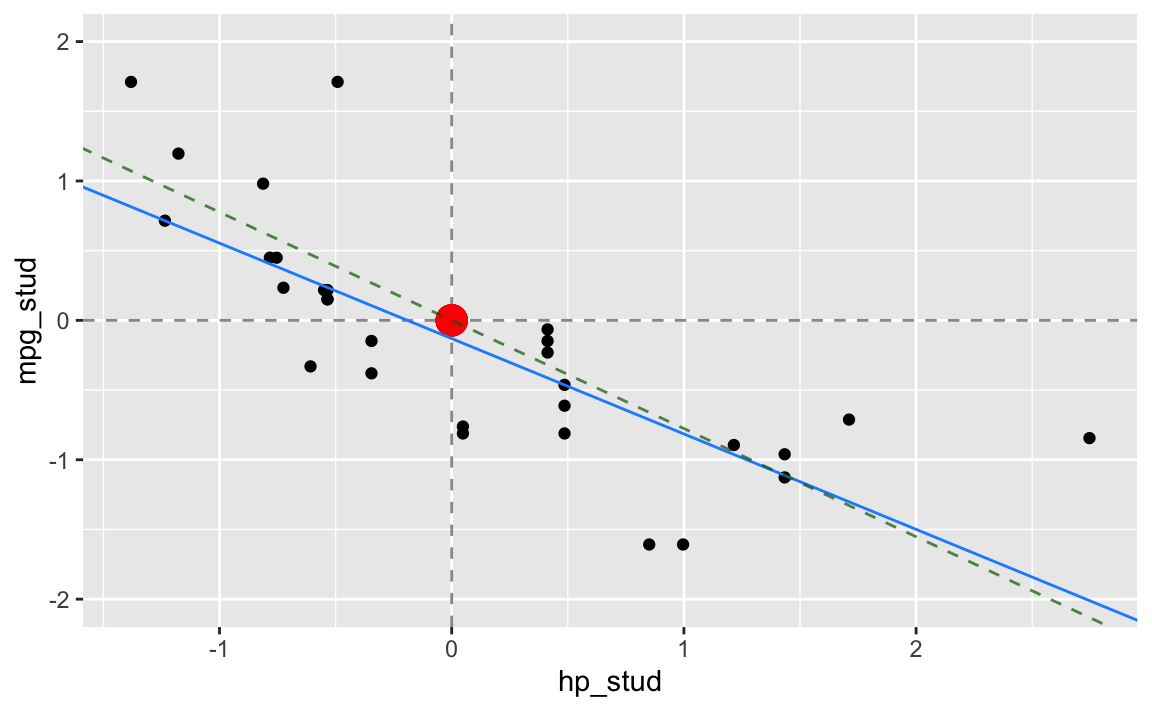
In grün und gestrichelt sehen wir die Gerade aus der Idee der quadratischen Abweichungssummen, in blau die aus der Idee der absoluten Abweichungssummen.
Für unser ursprüngliches Problem rechnen wir um:
# Umrechnen in die ursprüngliche Fragestellung
(as_b1 <- opti_as_beta_1 * sd(dt$mpg) / sd(dt$hp))
#> [1] -0.06016948
(as_b0 <- (mean(dt$mpg) - as_b1 * mean(dt$hp)) + opti_as_beta_0 * sd(dt$mpg))
#> [1] 28.13051Und die dazu gehörige Darstellung:
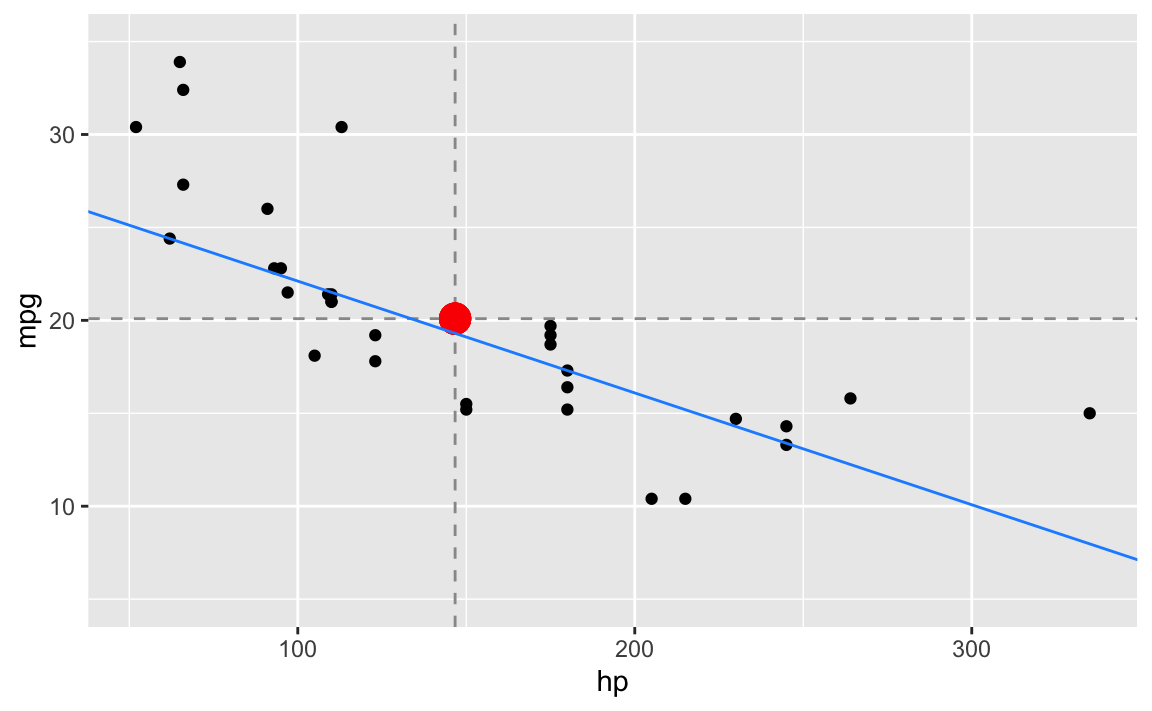
Die Funktionsvorschrift für die (blaue) Regressionsgerade lautet:
\[\begin{aligned} \hat{y} &= \hat\beta_0 + \hat\beta_1 \cdot x \\ &\approx 28.1305094 -0.0601695 \cdot x \\ &\approx 28.131 -0.06 \cdot x \end{aligned}\]
Diese Methode nennt sich Median-Regression und ein ein Spezialfall der Quantilsregression, die sich u.a. mit dem R-Paket quantreg unmittelbar umsetzen lässt:
library(quantreg)
ergmedianreg <- rq(mpg ~ hp, data = dt)
coef(ergmedianreg)
#> (Intercept) hp
#> 28.13050847 -0.060169491. Idee: Betrag der Summe der Abweichungen
Wenn wir die Summe der Abweichungen \(\sum\limits_{i=1}^n \hat{e}_i\) minimieren wollen, dann ist es sinnvoll den Betrag davon zu minimieren. Wir suchen also die Schätzer \(\hat\beta_0\) und \(\hat\beta_1\), so dass der Ausdruck
\[ \left| \sum_{i=1}^n \hat{e}_i \right| = \left| \sum_{i=1}^n (\hat\beta_0 + \hat\beta_1 \cdot x_i - y_i) \right| \]
minimal ist.
Wegen:
\[\begin{aligned} \sum_{i=1}^n (\hat\beta_0 + \hat\beta_1 \cdot x_i - y_i) &= \sum_{i=1}^n \hat\beta_0 + \sum_{i=1}^n \hat\beta_1 \cdot x_i - \sum_{i=1}^n y_i \\ &= n \cdot \hat\beta_0 + \hat\beta_1 \cdot \sum_{i=1}^n x_i - \sum_{i=1}^n y_i \\ &= n \cdot \hat\beta_0 + \hat\beta_1 \cdot n \cdot \bar{x} - n \cdot \bar{y} \\ &= n \cdot \left( \hat\beta_0 + \hat\beta_1 \cdot \bar{x} - \bar{y} \right) \\ &= n \cdot \left( \hat\beta_0 - \bar{y} + \hat\beta_1 \cdot \bar{x} \right) \end{aligned}\]
können wir das absolute Minimum bei \(\hat\beta_0 - \bar{y} =0\) und \(\hat\beta_1 \cdot \bar{x}=0\) erreichen, was zur Lösung \(\hat\beta_0 =\bar{y}\) und \(\hat\beta_1 = 0\) führt. Dies ist unser Nullmodel in dem die \(x_i\) keinen Einfluss auf die \(y_i\) haben und wir daher pauschal die \(y_i\) mit \(\hat{y}_i=\bar{y}\), also dem Mittelwert der \(y_i\) abschätzen.
Zusammenfassung
Als Vergleich können wir uns die Quadratsumme \(QS\) und Absolutsumme \(AS\) der drei Modelle einmal ansehen:
# Quadratische Abweichungssummen
qs <- function(b_0, b_1) {
sum(((b_0 + b_1 * dt$hp) - dt$mpg )**2)
}
# Absolute Abweichungssummen
as <- function(b_0, b_1) {
sum(abs((b_0 + b_1 * dt$hp) - dt$mpg))
}# Quadratsummen:
quad_sum <- c(qs(b0, b1), qs(as_b0, as_b1), qs(mean_mpg, 0))
# Absolutsummen:
abs_sum <- c(as(b0, b1), as(as_b0, as_b1), as(mean_mpg, 0))
tab <- tibble(
sums = c(quad_sum, abs_sum),
sum_type = rep(c("quad", "abs"), each = 3),
methode = rep(c("Idee 3", "Idee 2", "Idee 1"), 2)
)
pivot_wider(tab, names_from=sum_type, values_from=sums, names_sort=T)
#> # A tibble: 3 × 3
#> methode abs quad
#> <chr> <dbl> <dbl>
#> 1 Idee 3 93.0 448.
#> 2 Idee 2 87.3 477.
#> 3 Idee 1 151. 1126.Reproduzierbarkeitsinformationen
#> R version 4.1.2 (2021-11-01)
#> Platform: x86_64-apple-darwin17.0 (64-bit)
#> Running under: macOS Catalina 10.15.7
#>
#> Locale: de_DE.UTF-8 / de_DE.UTF-8 / de_DE.UTF-8 / C / de_DE.UTF-8 / de_DE.UTF-8
#>
#> Package version:
#> mosaic_1.8.3 quantreg_5.86 tidyr_1.1.4 xfun_0.29Das “Cookbook” zur Datentabelle können Sie mit Hilfe von
help("mtcars")aufrufen!↩︎