Datenjudo für Fragebögen
Ab und zu bekomme ich die Frage, wie man einen Fragebogen mit Likert-Scalen-Items auswerten kann.
Dazu kann etwas gezieltes Datenjudo helfen. Wir schauen uns das folgende generierte Mini-Beispiel an:
library(mosaic) # Basis Paket
library(tibble) # Eine modernere Variante der data.frames!
set.seed(2009) # Reproduzierbarkeit
N <- 25 # Anzahl der Testzeileneinträge in den "testdaten"!
# Wir wollen eine Likert-Scale
minLikert <- 1 # bis
maxLikert <- 6 # erstellen.
# Zum späteren Umrechnen der inversen Items:
maxInvItem <- maxLikert + 1
# Wir bauen uns eine Testumfrage mit zwei Itemserien
# (AS1-AS6 und BS1-BS6) und N Beobachtungen.
# Die Items AS3, AS4 und BS1 und BS5 sind dabei
# inverse Items, welche später umgerechnet werden:
testdaten <- tibble(
ID = 1:N,
# AS1-AS6 bilden ein Itemset:
AS1 = sample(minLikert:maxLikert, N, replace = TRUE),
AS2 = sample(minLikert:maxLikert, N, replace = TRUE),
AS3 = sample(minLikert:maxLikert, N, replace = TRUE),
AS4 = sample(minLikert:maxLikert, N, replace = TRUE),
AS5 = sample(minLikert:maxLikert, N, replace = TRUE),
AS6 = sample(minLikert:maxLikert, N, replace = TRUE),
# BS1-BS5 bilden ein Itemset:
BS1 = sample(minLikert:maxLikert, N, replace = TRUE),
BS2 = sample(minLikert:maxLikert, N, replace = TRUE),
BS3 = sample(minLikert:maxLikert, N, replace = TRUE),
BS4 = sample(minLikert:maxLikert, N, replace = TRUE),
BS5 = sample(minLikert:maxLikert, N, replace = TRUE),
# Geschlecht als sex mit (1 für Frauen und 2 für Männer)
sex = sample(1:2, N, replace = TRUE)
)
# Orinal testdaten einmal ausgeben:
head(testdaten)
#> # A tibble: 6 × 13
#> ID AS1 AS2 AS3 AS4 AS5 AS6 BS1 BS2 BS3 BS4 BS5 sex
#> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
#> 1 1 4 4 1 1 2 4 5 5 3 2 3 2
#> 2 2 2 1 2 2 5 6 4 5 2 2 6 1
#> 3 3 4 4 6 3 3 4 3 3 4 1 5 1
#> 4 4 2 6 1 4 5 4 6 4 5 1 3 1
#> 5 5 3 1 3 5 5 6 6 1 2 6 5 1
#> 6 6 6 4 1 3 6 6 4 6 5 3 3 1Die Spalten AS3, AS4 und BS1, BS5 waren inverse Items, die wir noch umrechnen müssen:
# Inverse Item umrechnen:
testdaten |>
mutate(
AS3 = maxInvItem - AS3,
AS4 = maxInvItem - AS4,
BS1 = maxInvItem - BS1,
BS5 = maxInvItem - BS5
) -> testdaten_korrigiert
# Die Daten mit den umgerechnetern inversen Items:
head(testdaten_korrigiert)
#> # A tibble: 6 × 13
#> ID AS1 AS2 AS3 AS4 AS5 AS6 BS1 BS2 BS3 BS4 BS5 sex
#> <int> <int> <int> <dbl> <dbl> <int> <int> <dbl> <int> <int> <int> <dbl> <int>
#> 1 1 4 4 6 6 2 4 2 5 3 2 4 2
#> 2 2 2 1 5 5 5 6 3 5 2 2 1 1
#> 3 3 4 4 1 4 3 4 4 3 4 1 2 1
#> 4 4 2 6 6 3 5 4 1 4 5 1 4 1
#> 5 5 3 1 4 2 5 6 1 1 2 6 2 1
#> 6 6 6 4 6 4 6 6 3 6 5 3 4 1Die jeweiligen Itemsets werden nun zur einem Wert (Gesamtscore)
zusammengefasst, in dem wir jeweils den Mittelwert von AS1-AS6
und BS1-BS5 bildenund in AS bzw. BS speichern:
# Wir fassen nun die AS1-AS6 und die BS1-BS5 zusammen
# und bilden die jeweiligen Mittelwerte:
testdaten_korrigiert |>
group_by(ID, sex) |> # Damit wird für jede Zeile die Zusammenfassung gemacht!
summarise(
AS = mean(c(AS1, AS2, AS3, AS4, AS5, AS6)),
BS = mean(c(BS1, BS2, BS3, BS4, BS5))
) -> testdaten_sum
# Ausgabe der Mittelwerte der AS und BS
head(testdaten_sum)
#> # A tibble: 6 × 4
#> # Groups: ID [6]
#> ID sex AS BS
#> <int> <int> <dbl> <dbl>
#> 1 1 2 4.33 3.2
#> 2 2 1 4 2.6
#> 3 3 1 3.33 2.8
#> 4 4 1 4.33 3
#> 5 5 1 3.5 2.4
#> 6 6 1 5.33 4.2Die Datentabelle testdaten_sum enthält nun die Spalten AS und BS mit den entsprechenden Mittelwerten der einzelnen Items AS1-AS6 sowieso BS1- BS5.
Wir wollen nun die Ergebnisse als Boxplots anzeigen lassen. Dafür benennen wir die Geschlechter von 1,2 auf “Frau”, “Mann” um:
testdaten_sum |>
mutate(sex = factor(sex, levels = c(1, 2),
labels = c("Frau", "Mann"))
) -> testdaten_sex Nun können wir die Boxplots erstellen:
# Darstellung der Ergebnisse als Boxplot AS ~ sex:
gf_boxplot(AS ~ sex, data = testdaten_sex) %>%
gf_labs(
title = "Boxplot von AS nach Geschlechtern",
x = "Geschlechter",
y = "Item AS"
) |>
gf_refine(
scale_y_continuous(
breaks = 1:6,
label = 1:6,
limits = c(2.5, 4.5) # Gibt den Bereich von 2.5 bis 4.5 aus!
)
)
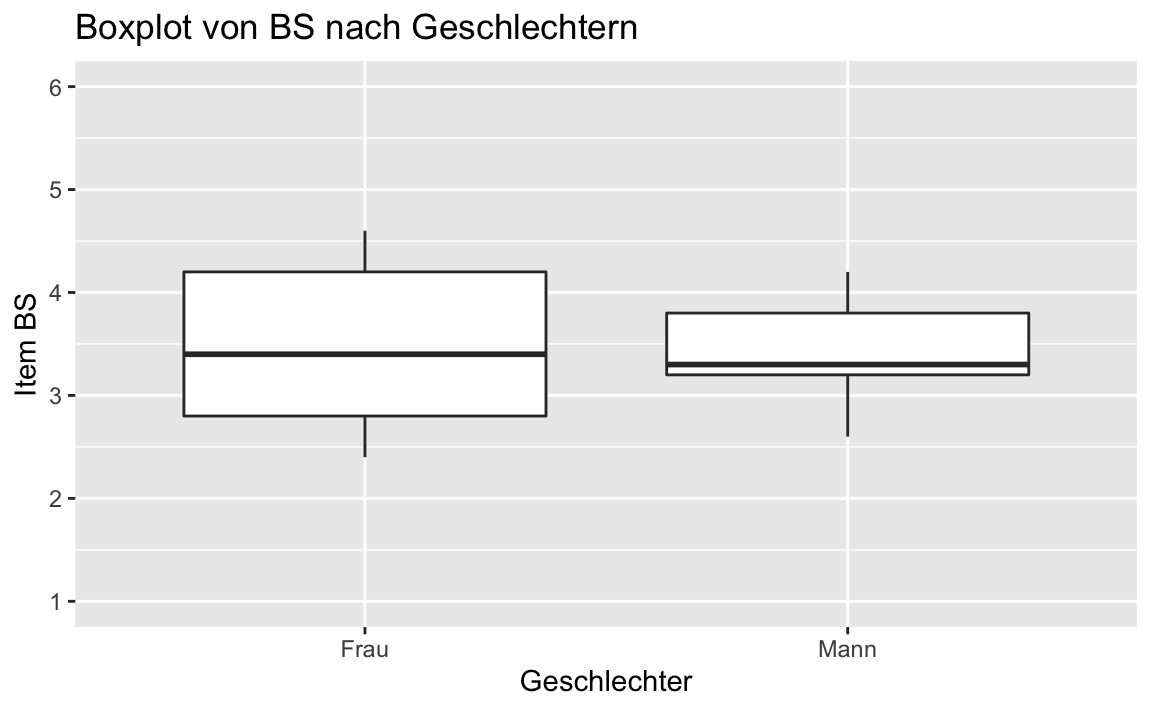
# Darstellung der Ergebnisse als Boxplot BS ~ sex:
gf_boxplot(BS ~ sex, data = testdaten_sex) %>%
gf_labs(
title = "Boxplot von BS nach Geschlechtern",
x = "Geschlechter",
y = "Item BS"
) |>
gf_refine(
scale_y_continuous(
breaks = 1:6,
label = 1:6,
limits = c(1, 6) # Gibt den ganzen Bereich von 1 bis 6 aus!
)
)
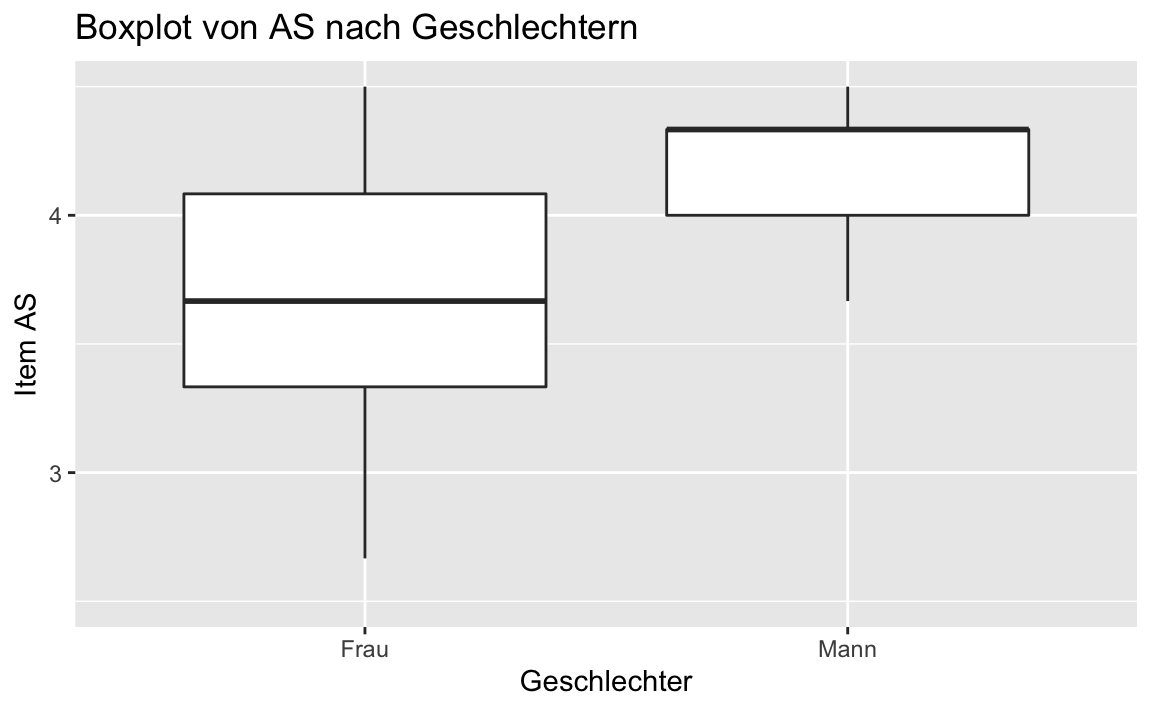
Die Kennzahlen dazu erhalten wir mit favstats. Dabei wählen wir die ersten sechs Einträge (Variabelbezeichnung und Q0 bis Q4) aus:
favstats(AS ~ sex, data = testdaten_sex)[1:6]
#> sex min Q1 median Q3 max
#> 1 Frau 2.166667 3.333333 3.666667 4.166667 5.333333
#> 2 Mann 3.666667 4.000000 4.333333 4.333333 4.500000
favstats(BS ~ sex, data = testdaten_sex)[1:6]
#> sex min Q1 median Q3 max
#> 1 Frau 2.4 2.8 3.4 4.2 4.6
#> 2 Mann 2.6 3.2 3.3 3.8 4.2Unter der Verwendung des Pakets likert (https://github.com/jbryer/likert) können wir die Ausgaben auch noch etwas schöner gestalten:
library(likert)
# Wir wählen nur den Itemset BS aus und speichern in in items2:
testdaten_korrigiert |>
select(
starts_with("BS")
) -> items2
# Leider mag likert tibbels nicht so gerne, daher:
items2 <- as.data.frame(items2)
# Wir geben den Items noch ein paar Buzzwords:
names(items2) <- c("Gesundheit", "Familie", "Geld", "Freunde", "Langes Leben")
# Vorbereitung:
l2 <- likert(items2, nlevels = 5)
# Zusammenfassung
summary(l2)
#> Item low neutral high mean sd
#> 3 Geld 28.57143 23.809524 47.61905 3.380952 1.359272
#> 5 Langes Leben 57.14286 4.761905 38.09524 2.619048 1.532194
#> 1 Gesundheit 38.09524 28.571429 33.33333 2.857143 1.492840
#> 2 Familie 38.09524 28.571429 33.33333 2.952381 1.499206
#> 4 Freunde 42.85714 23.809524 33.33333 2.857143 1.236354
# Graphische Ausgaben:
plot(l2)
plot(l2,"bar")
plot(l2,"heat")
plot(l2,"density")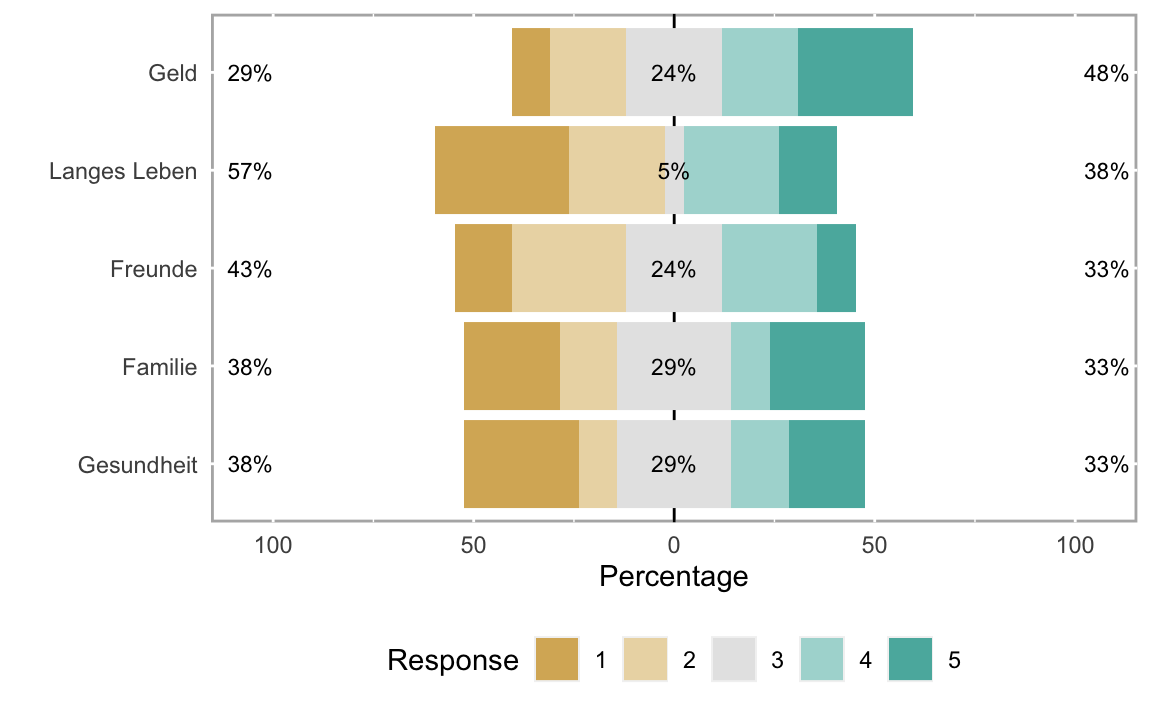
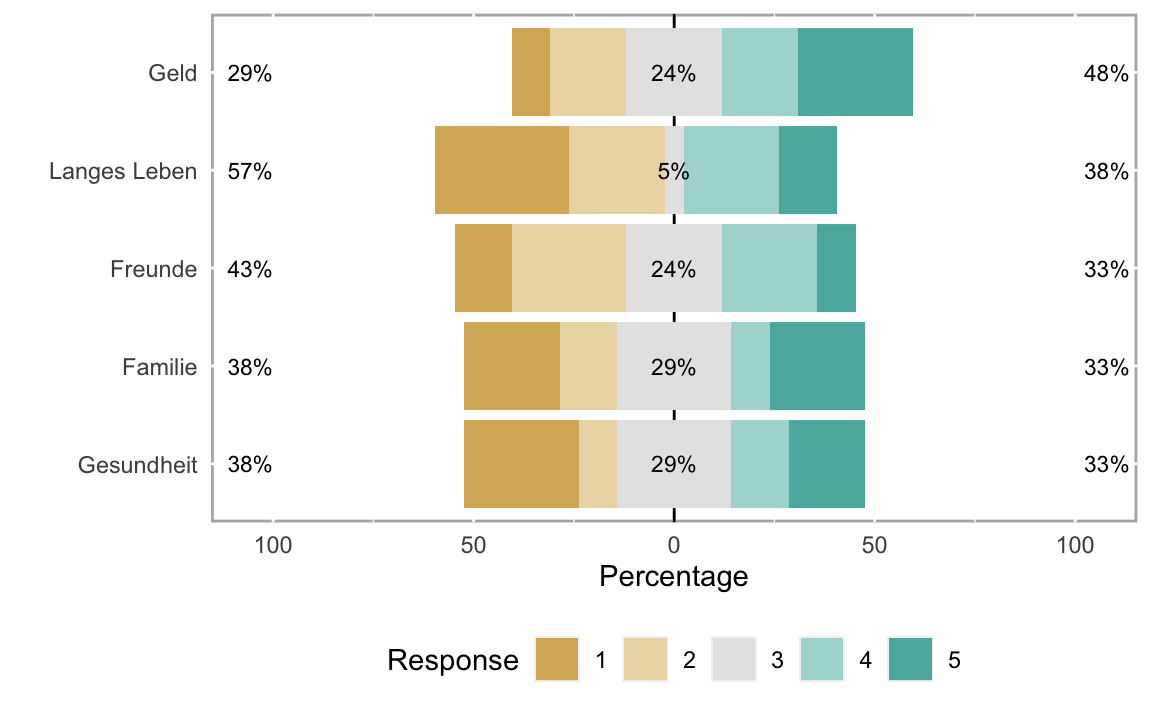
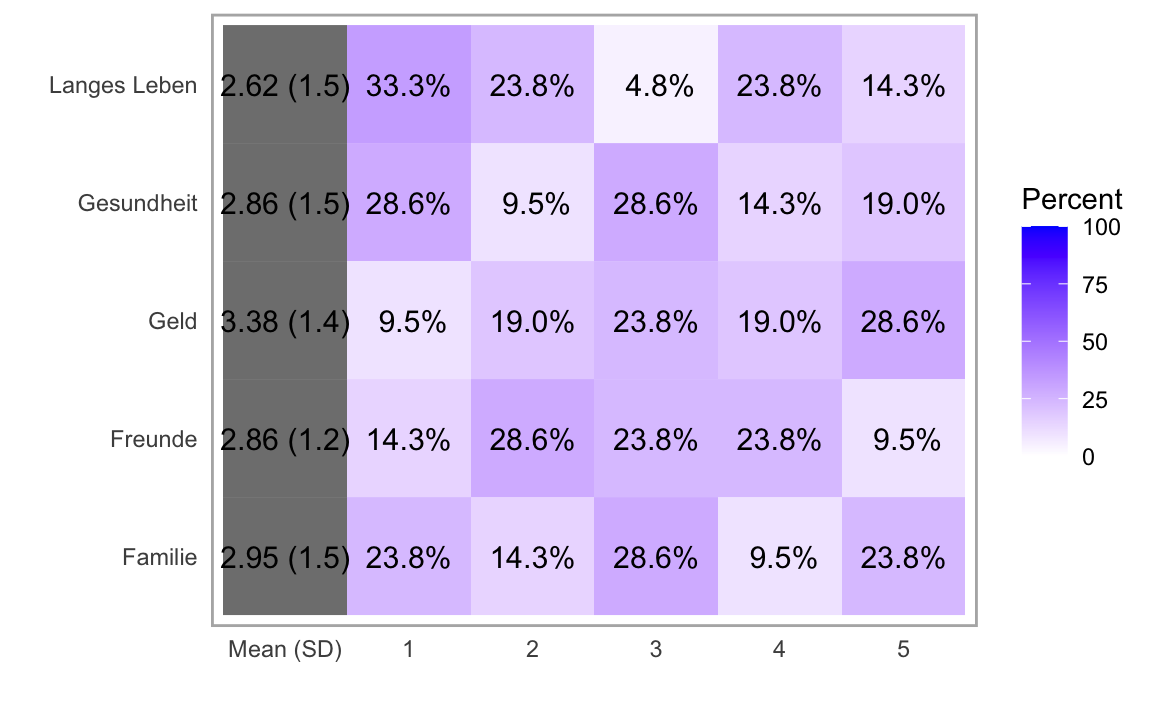
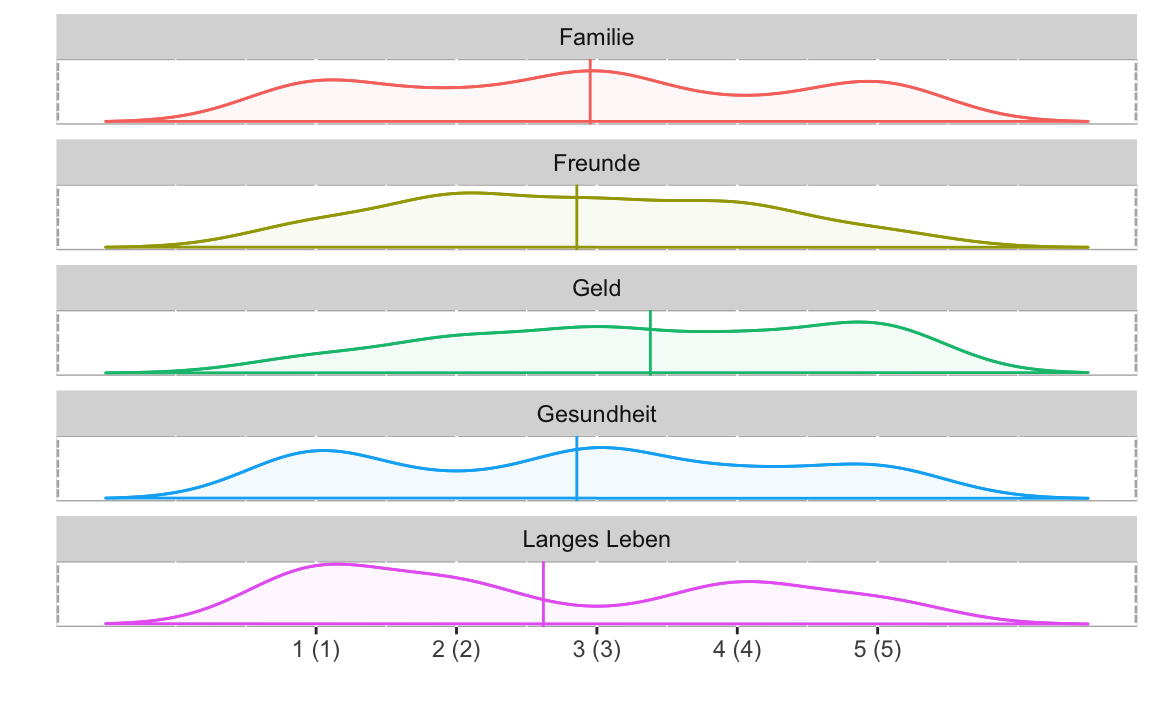
Voilà!
Norman Markgraf
Diplom-Mathematiker
Norman Markgraf ist freiberuflicher Dozent für Mathematik, Statistik, Data Science und Informatik, sowie freiberuflicher Programmierer.