Ein paar Gedanken über potenzgesetzliche Verteilungen (power law distributions)

Eine Funktion \(f(x)\) heißt potenzgesetzlich, falls

\[f(x) = C \cdot x^a\]

gilt, für mindestens alle reellen \(x > x_{min}\).

Gewöhnlich setzt man \(\alpha = -a\) und schreibt

\[f(x) = C \cdot x^{-\alpha}.\]

Damit ergibt sich für \(f'(x)\) die Form:

\[ f'(x) = -C \cdot \alpha \cdot x^{-\alpha -1} = C^* \cdot x^{-(\alpha + 1)} \] mit \(C^* = -C \cdot \alpha\).

Eine (streng) potenzgesetzliche Verteilungen (engl. (strong) power-law probability distribution) zur ZV \(X\) ist eine Verteilung deren Überlebensfunktion \(\overline{F}_X(x)=P(X > x)\) die folgende Gestalt hat: \[\overline{F}(x)=P(X > x) = C \cdot x^{-\alpha}\]

Mit der Dichte \(f_X\) ergibt sich: \[\overline{F}(x)=P(X > x) = C \cdot x^{-\alpha} =\int_x^\infty f_X(t) \text{d}t = C^* \cdot \int_x^\infty t^{-(\alpha+1)} \text{d}t = C^* \cdot \int_x^\infty t^{-\alpha} \text{d}t\]

Anstelle der Konstanten \(C\) tritt oft eine langsam variierende Funktion (engl. slowly varying funktion). Wir erhalten somit die folgende, allgemeinere Definition:

Eine potenzgesetzliche Verteilungen (engl. power-law probability distribution) (zu einer Zufallsvariable \(X\)) ist eine Verteilung deren Überlebensfunktion \(\overline{F}(x)=P(X > x)\) die folgende Gestalt hat:

\[\overline{F}(x)=P(X > x) = L(x) \cdot x^{-\alpha}\]

Dabei ist \(L(x):(x_{\min}, +\infty) \to (x_{\min}, +\infty)\) eine langsam variierende Funktion, also gilt für alle \(t>0\):

\[ \lim_{x \to +\infty} \frac{L(t \cdot x)}{L(x)} = 1 \]

Ist nun wieder \(f_X\) die Dichte, so erhalten wir: \[\overline{F}(x)=P(X > x) = L(x) \cdot x^{-\alpha} = \int_x^\infty f_X(t) dt\]

\[f'(x) = [L(x)x^{-\alpha}]'\] \[\int_x^\infty f_X(t) dt= \int_x^\infty [L(t)t^{-\alpha}]' dt\]

\(\Delta x_0 = h = x_1 - x_0\) \(x_1 = x_0 + \Delta x_0 = x_0 + h\) \(x_1 = c \cdot x_0\) \(x_0 + h = c \cdot x_0 <=> c = 1 + \frac{h}{x_0}\) \(L(x_1) = L(x_0+h) = L(c \cdot x_0)\) \(L(x_1) - L(x_0) = L(c \cdot x_0) - L(x_0) = L(x_0 + h) - L(x_0)}\) $

Fakten:

• Sinnvoll nur, wenn \(\alpha > 0\).
• Ist \(\alpha < 3\), dann ist die Varianz und die Schiefe (engl. skewness) (mathematisch) nicht definiert.
• Für \(k > \alpha-1\) ist das k. Moment unendlich.

Logarithmiert man \(y=f(x)=C \cdot x^{-\alpha}\), so erhält mensch:

\[\log(y) = \log(C) -\alpha \cdot \log(x)\]

Ist eine Verteilung potenzgesetzlich, dann kann man \(\alpha\), wie folgt abschätzen:

Seien \(x_0, x_1 > x_{min}\) zwei reelle Zahlen, \(y_0=f(x_0)\) bzw. \(y_1 = f(y_1)\).

Dann kann mensch wegen

\[\begin{align*} \log(y_1) - \log(y_0) &= \log(C) - \alpha \cdot\log(x_1) - \log(C) + \alpha \cdot \log(x_0) \\ &= \alpha \cdot\left(\log(x_0)- \log(x_1) \right) \end{align*}\]

den Wert für \(\alpha\), so kann man mittels

\[\alpha = \frac{\log(y_1) - \log(y_0)}{\log(x_0)- \log(x_1)}\]

den Wert für \(\alpha\) bestimmen.

Mit dem so ermittelten \(\alpha\), können wir \(C\) wegen

\[\log(C) = \log(y)+ \alpha\log(x)\]

mit Hilfe von

\[C = y \cdot x_0^\alpha = f(x_0) \cdot x_0^\alpha\]

für ein \(x_0 > x_{min}\) abschätzen.

Beispiel:

Nehmen wir die t-Verteilung mit \(n=2\) Freiheitsgeraden. Die Dichtefunktion bezeichnen wir mit \(t_{2}(x)\).

Dann dann können wir \(\alpha=3\) und \(C=1\) abschätzen.

Schauen wir uns das einmal als Grafik an:

lower_bound <- 2
upper_bound <- 100
x <- seq(lower_bound, upper_bound, 0.1)

gf_dist("t", df = dfree, 
        xlim = c(lower_bound, upper_bound), 
        color = "darkred") %>%
  gf_line(C*x**(-alpha) ~ x, 
          color = "darkgreen")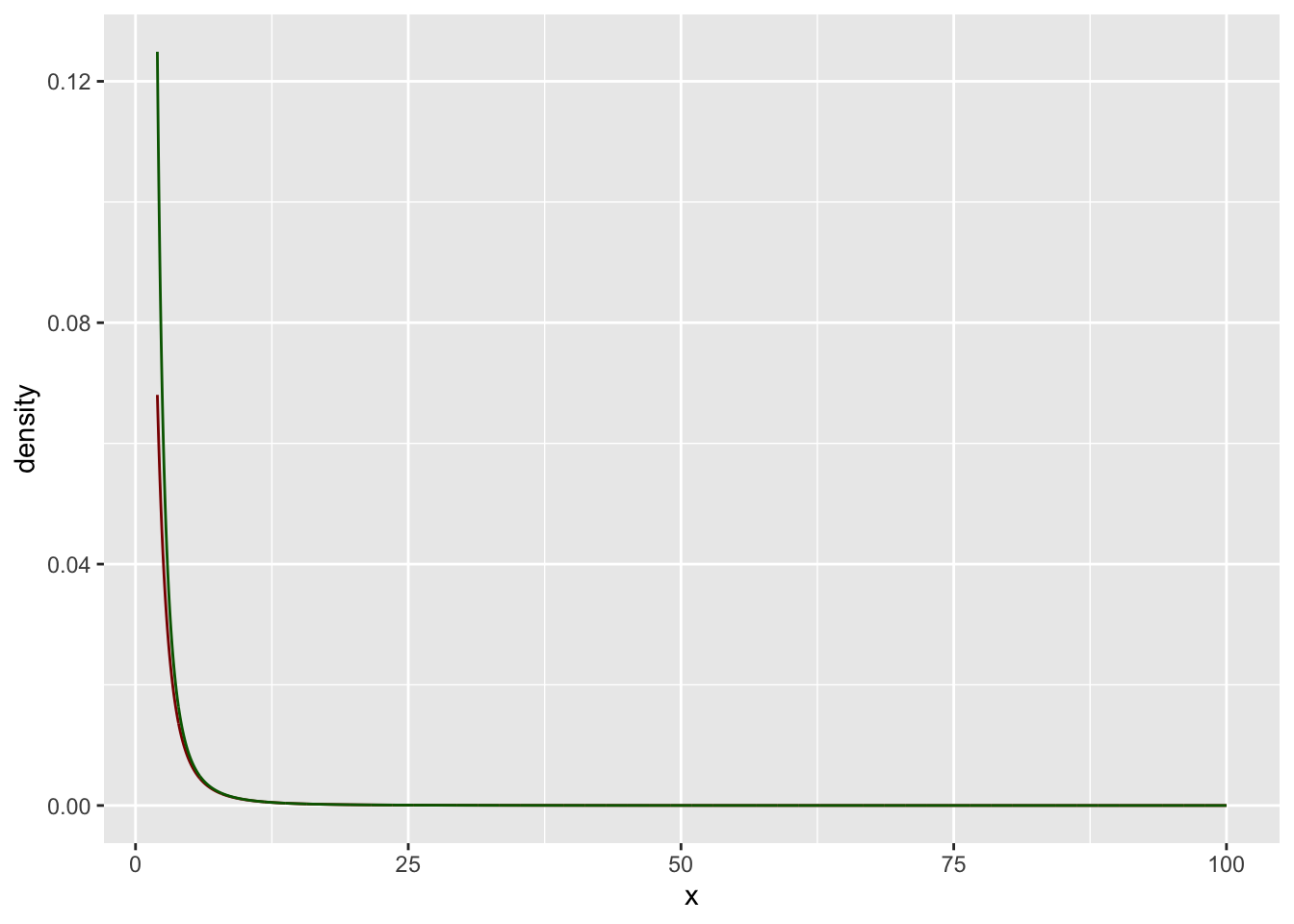

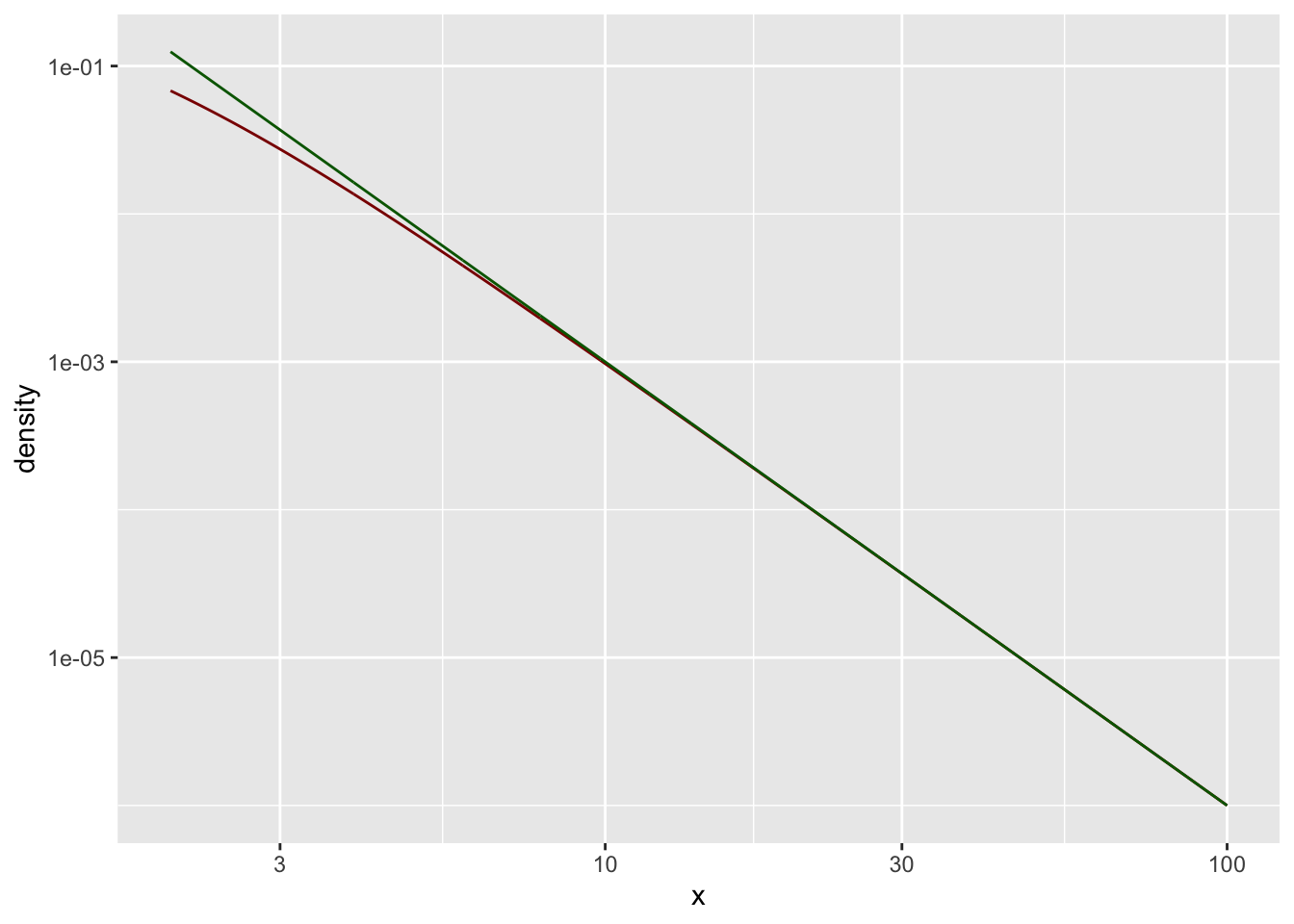
Hier eine doppelt-logarithmische Darstellung:

gf_dist("t", df = dfree, 
        xlim = c(lower_bound, upper_bound), 
        color = "darkred") %>%
  gf_line( C*x**(-alpha) ~ x, 
           color = "darkgreen") %>%
  gf_refine(
    scale_x_log10(),
    scale_y_log10()
  )

Noch ein Beispiel:

Nehmen wir die t-Verteilung mit \(n=1\) Freiheitsgeraden. Die Dichtefunktion bezeichnen wir mit \(t_{1}(x)\).

Dann dann können wir \(\alpha=2\) und \(C=0.32\) abschätzen.

Schauen wir uns das einmal als Grafik an:

lower_bound <- 2
upper_bound <- 100
x <- seq(lower_bound, upper_bound, 0.1)

gf_dist("t", df = dfree, 
        xlim = c(lower_bound, upper_bound), 
        color = "darkred") %>%
  gf_line(C*x**(-alpha) ~ x, 
          color = "darkgreen")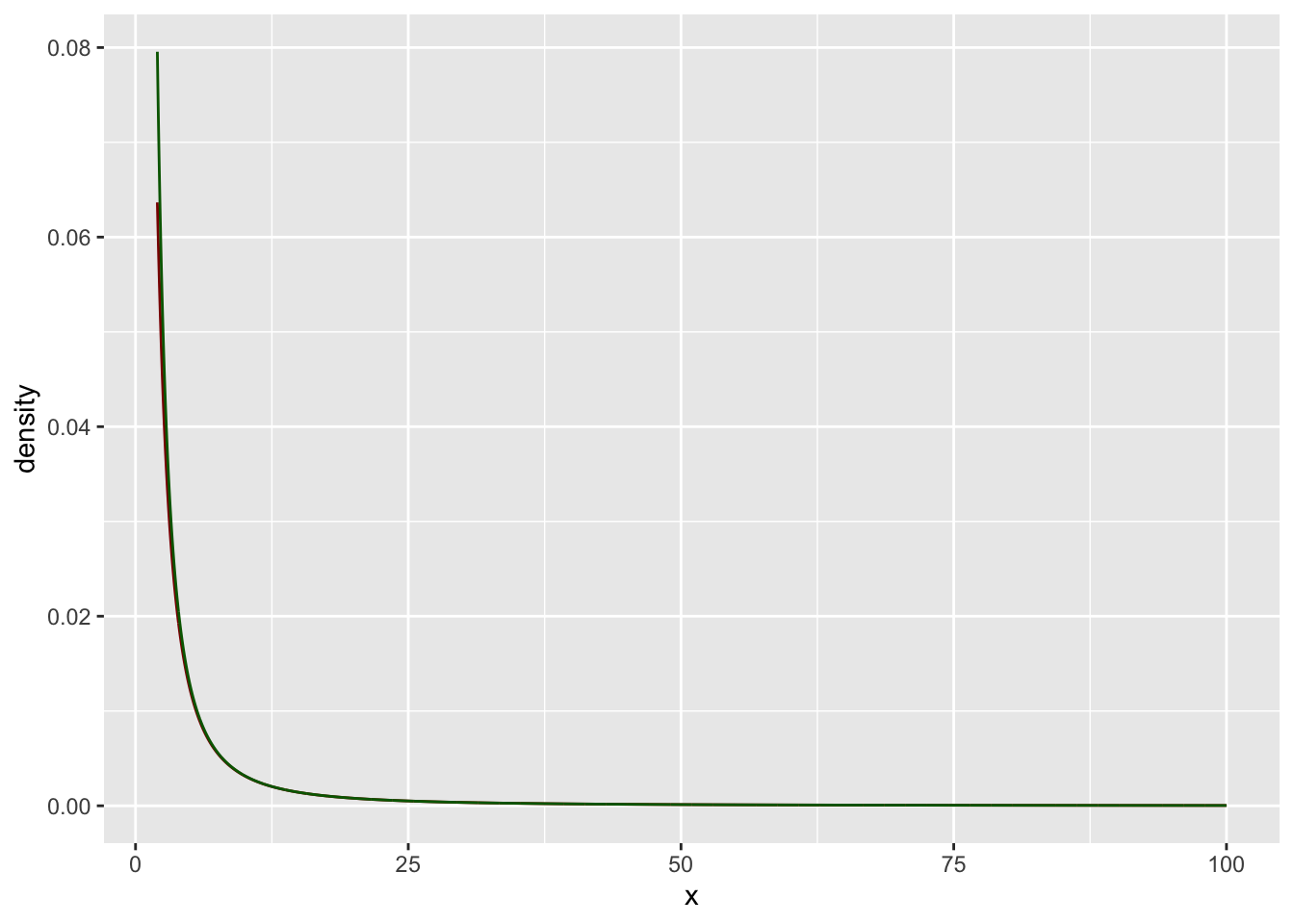

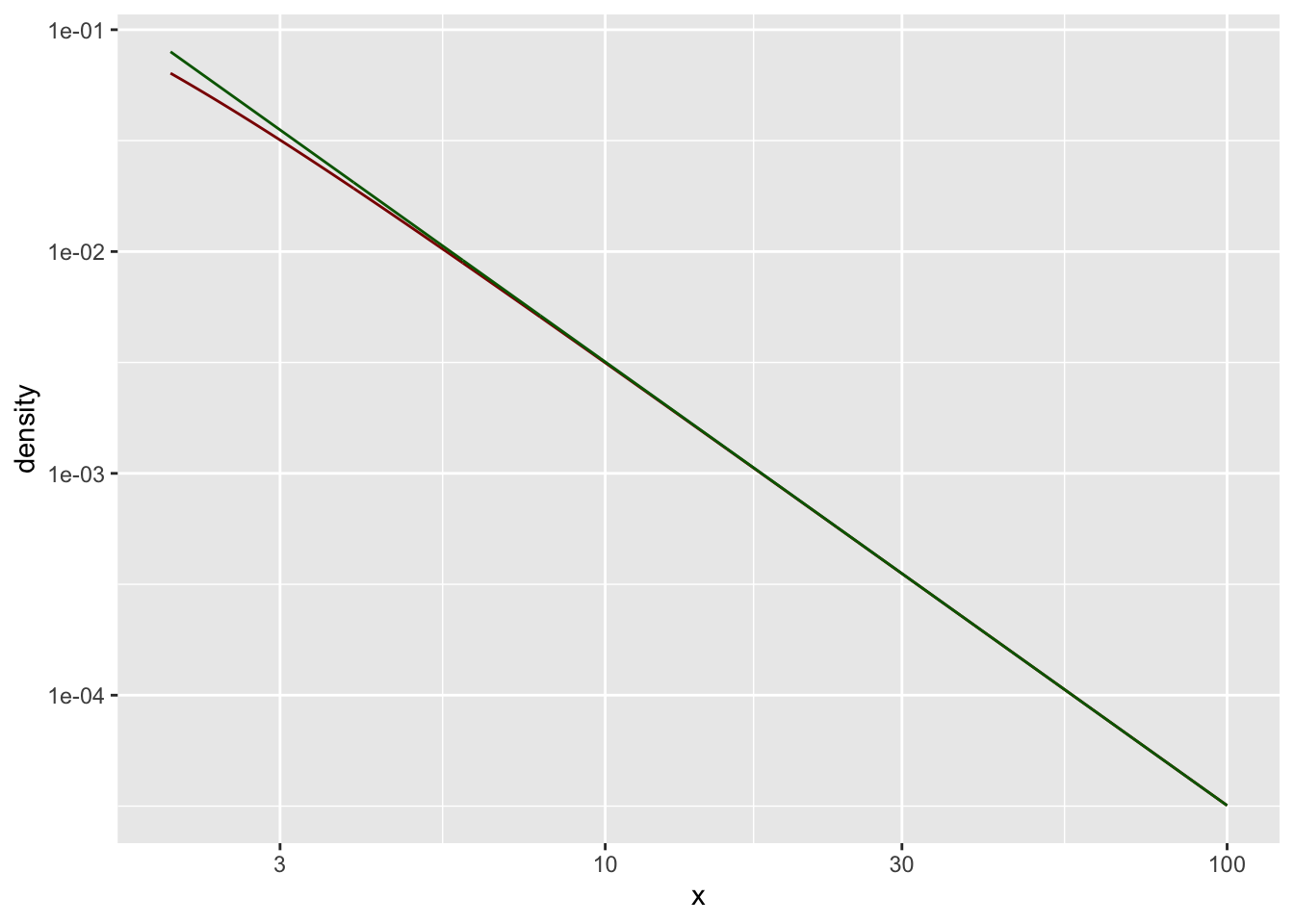
Hier eine doppelt-logarithmische Darstellung:

gf_dist("t", df = dfree, 
        xlim = c(lower_bound, upper_bound), 
        color = "darkred") %>%
  gf_line( C*x**(-alpha) ~ x, 
           color = "darkgreen") %>%
  gf_refine(
    scale_x_log10(),
    scale_y_log10()
  )

Ein ’Gegen-’Beispiel:

Betrachten wir nun die (rechte Seite – \(x>1=x_{min}\)) einer Gauß’schen Standardnormalverteilung.

Mit den Stützstellen \(x_0 = 1\) und \(x_1 = 5\) können wir \(\alpha=7.46\) und \(C=0.24\) abschätzen. Schauen wir uns das einmal als Grafik an:

lower_bound <- 1
upper_bound <- 8
x <- seq(lower_bound, upper_bound, 0.1)

gf_dist("norm",
        xlim = c(lower_bound, upper_bound), 
        color = "darkred") %>%
  gf_line(C*x**(-alpha) ~ x, 
          color = "darkgreen")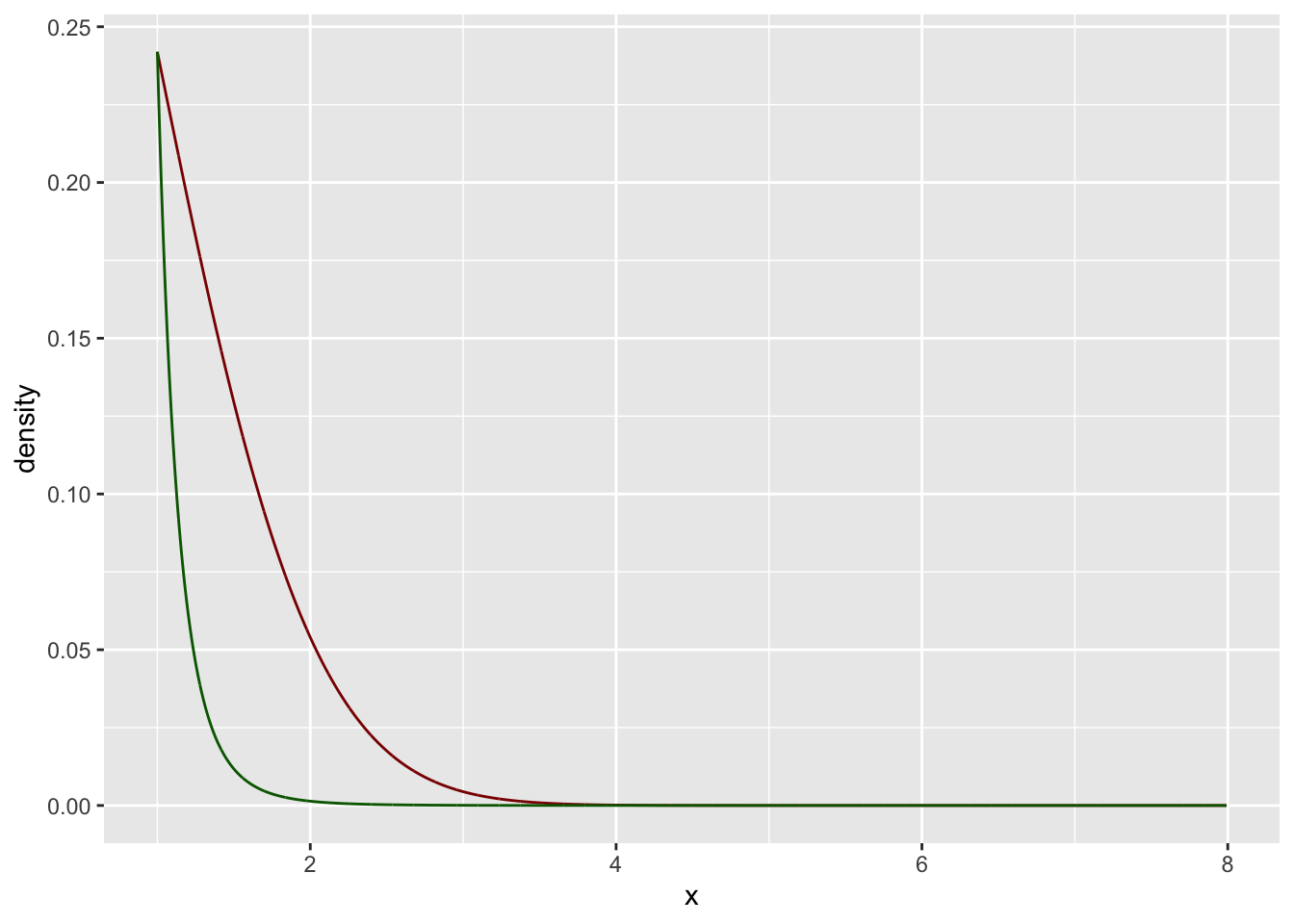

Hier eine doppelt-logarithmische Darstellung:

gf_dist("norm", 
        xlim = c(lower_bound, upper_bound), 
        color = "darkred") %>%
  gf_line( C*x**(-alpha) ~ x, 
           color = "darkgreen") %>%
  gf_refine(
    scale_x_log10(),
    scale_y_log10()
  )

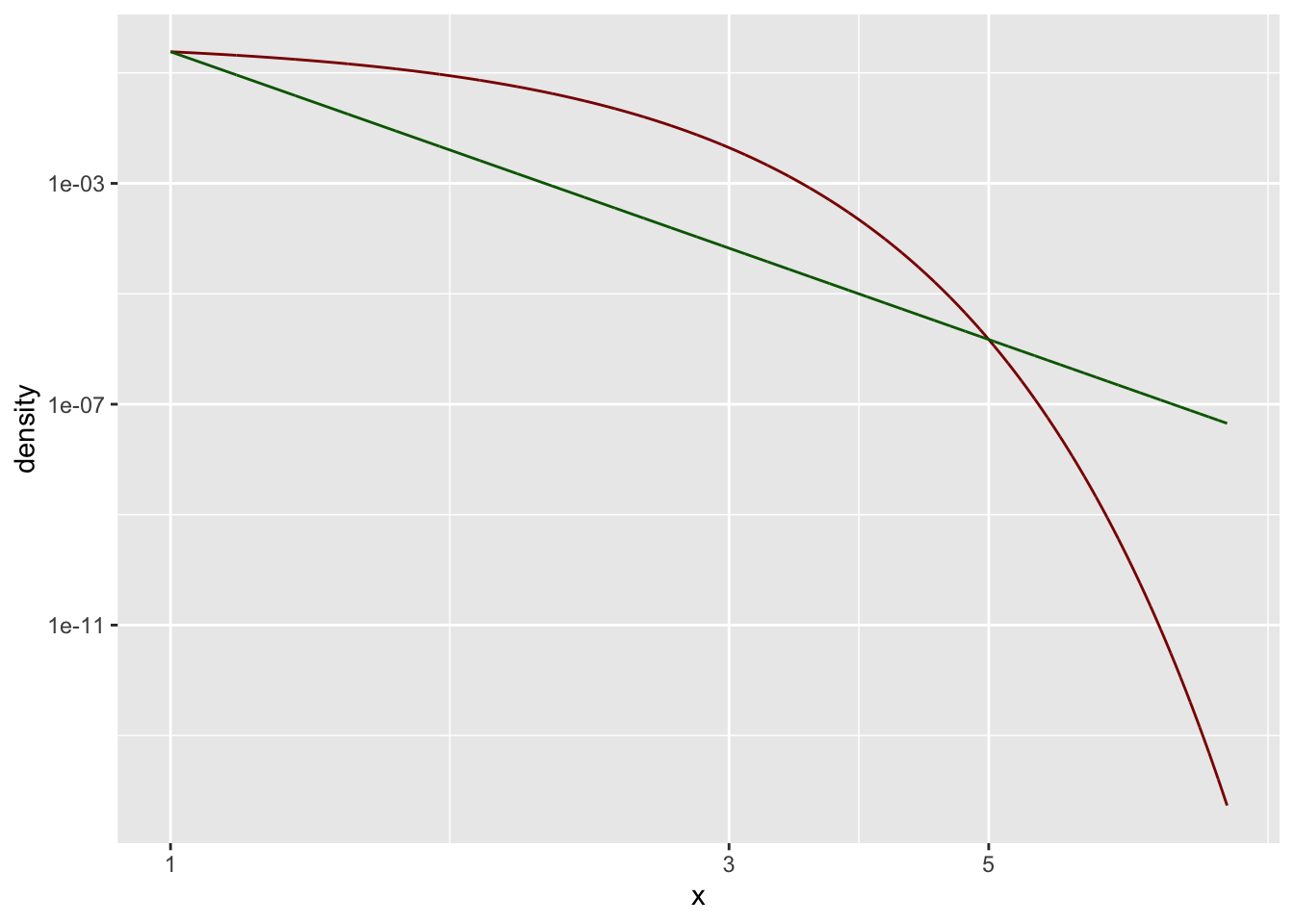
Wir erkennen, dass hier etwas nicht passt. Die Standardnormalverteilung ist (vielleicht) keine potenzgesetzich Verteilung?

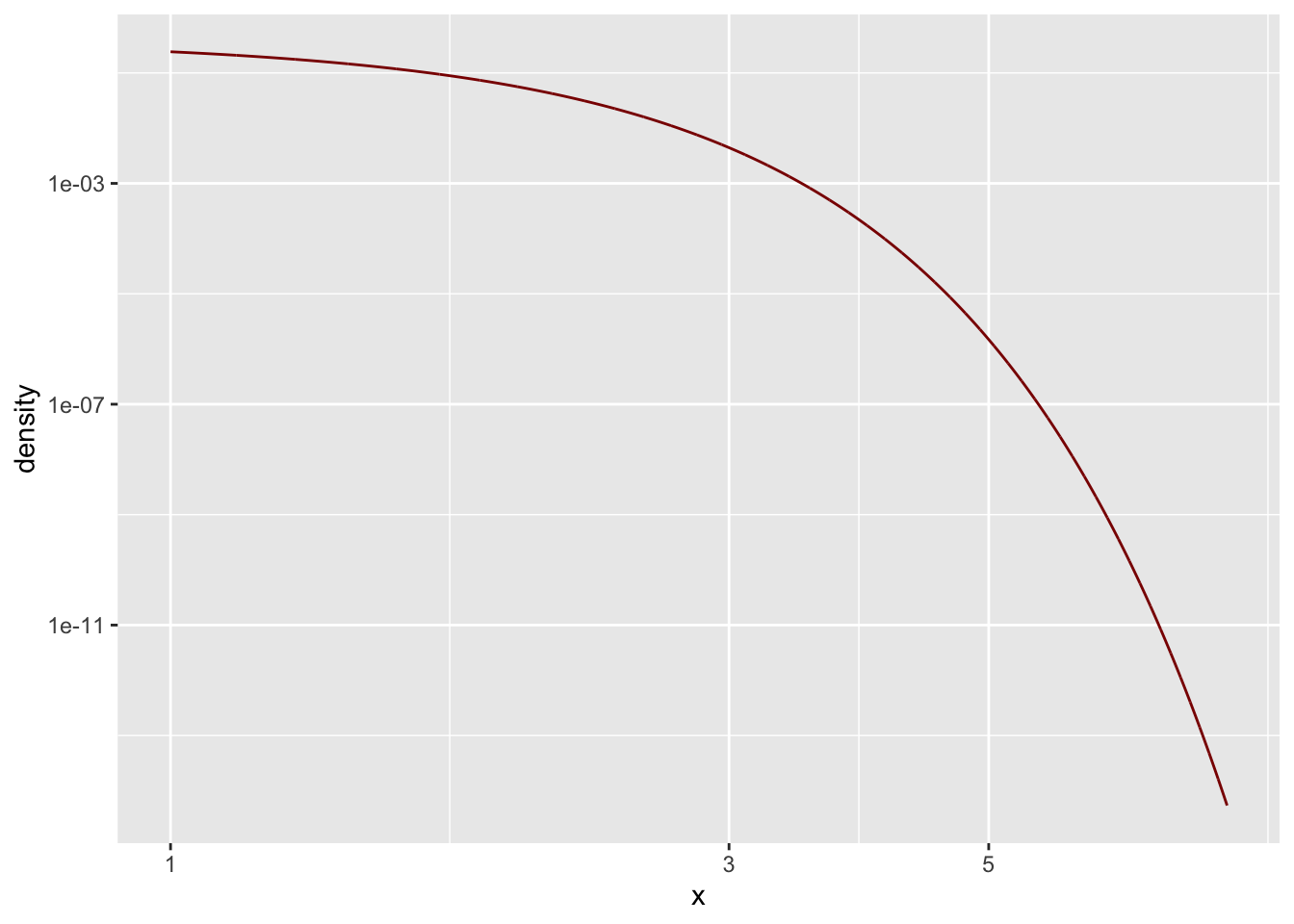
Ein oft verwendetes Kriterium ist, dass sich die Funktion in der doppelt-logarithmischen Darstellung als Gerade offenbart.

Schauen wir daher einmal nach:

lower_bound <- 1
upper_bound <- 8

gf_dist("norm", 
        xlim = c(lower_bound, upper_bound), 
        color = "darkred") %>%
  gf_refine(
    scale_x_log10(),
    scale_y_log10()
  )

** — **

Weiter gilt für potenzgesetzliche Verteilungen wegen

\[\frac{f(x)}{f(c\cdot x)} = \frac{C \cdot x^{-\alpha}}{C \cdot (c\cdot x)^{-\alpha}} = c^\alpha\]

\(f(x)\) und \(f(c\cdot x)\) für alle (beliebig aber festen) \(c>0\) proportional, was man gerne als \(f(x) \propto f(c \cdot x)\) schreibt.

** — **

Die Wahrscheinlichkeit für ein (mindestens) \(8-\sigma\) Ereignis liegt bei einer Standardnormalverteilung bei etwa \(6.66133814775094\times 10^{-16}\).

Bei einer t-Verteilung mit 2 Freiheitsgeraden bei etwa 0.00763403608266899$.

Während die Eintrittschance eines (mindestens) \(8-\sigma\) Ereignisses bei der Standardnormalverteilung bei etwa \(1 : round(1/(1-pnorm(8)),0)\) liegt, ist diese der t-Verteilung mit einem Freiheitsgrad bei etwa $1 : 131