Über die t-Verteilung mit einem bzw. zwei Freiheitsgraden

Vorbereitungen für R

Für die graphischen Ausgaben nutzen wir R und das Paket mosaic:

library(mosaic)

Vorbemerkungen und Notationen

Da alle t-Verteilungen symmetrisch sind, betrachten wir im wesendlichen nur den positiven Teil.

Zwei reelle Funktionen \(f\), \(g\) sind genau dann, im Sinne von de Bruijn¹ (§1.4), asymptotisch äquivalent \(f \sim g\), wenn

\[ \lim\limits_{x \to \infty} \frac{f(x)}{g(x)} = 1 \]

gilt.

Ist \(f \sim g\), so können wir auch

\[ f(x) = g(x)\cdot(1+o(1)) \]

dafür schreiben. Dabei ist \(h(x) = o(\phi(x))\) für \(x \to \infty\), falls \(\lim\limits_{x \to \infty} \frac{h(x)}{\phi(x)} = 0\) gilt. Aus der asymptotischen Äquivalenz von \(f\) und \(g\) folgt nun direkt:

\[ \lim\limits_{x \to \infty}\frac{f(x)}{g(x)}-1 =\frac{f(x)-g(x)}{g(x)} = 0 \]

Mit \(h(x) = \frac{f(x)-g(x)}{g(x)}\) ist \(h(x) = o(1)\) und daher \(f(x)-g(x) = g(x)o(1)\) und schliesslich \(f(x) = g(x)+g(x)o(1)\).

Ein wichtiges Korrolar sagt:

Ist \(f \sim g\), so ist auch \(\log(f) \sim \log(g)\).

Die t-Verteilung im Allgemeinen

Die Dichtefunktion der t-Verteilung lauten im Allgemeinen:

\[ f_n(x) = \frac{\Gamma\left(\frac{n+1}{2}\right)} {\sqrt{n\pi}~\Gamma\left(\frac{n}{2}\right)}\left(1+\frac{x^{2}}{n}\right)^{-\frac{n+1}{2}}\quad \mathrm{für}\quad -\infty < x < +\infty \]

wobei wir mit \(\Gamma(x)\) die Gammafunktion

\[ \Gamma(x)=\int\limits_{0}^{+\infty}t^{x-1}e^{-t}\operatorname{d}t \]

bezeichnen. Für einige \(x\) nimmt die Gammafunktion leicht zu berechnende Werte an:

So ist für alle \(n\in\mathbf{N_0}\):

\(\Gamma(n+1) = n!\) und \(\Gamma\left(n + \frac{1}{2}\right) = \frac{(2n)!}{n!4^n}\sqrt{\pi}\)

mit der gewöhnlichen Fakultät \(n! = \prod_{i=0}^n i\), wobei per Definition \(0!=1\) ist.

Die t-Verteilung mit einem Freiheitsgrad

Für \(f_1(x)\) ergibt sich somit:

\[ \begin{align*} f_1(x) &= \frac{\Gamma\left(\frac{n+1}{2}\right)} {\sqrt{n\pi}~\Gamma\left(\frac{n}{2}\right)}\left(1+\frac{x^{2}}{n}\right)^{-\frac{n+1}{2}} \\ &= \frac{\Gamma\left(\frac{2}{2}\right)} {\sqrt{\pi}~\Gamma\left(\frac{1}{2}\right)}\left(1+x^{2}\right)^{-\frac{2}{2}} \\ &= \frac{\Gamma\left(1\right)} {\sqrt{\pi}~\Gamma\left(\frac{1}{2}\right)}\left(1+x^{2}\right)^{-1} \\ \end{align*} \]

Wegen \(\Gamma(1) = 0! = 1\) und \(\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}\) ergibt sich nun:

\[ \begin{align*} f_1(x) &= \frac{1} {\sqrt{\pi} \cdot \sqrt{\pi}} \cdot \left(1+x^{2}\right)^{-1} \\ &= \frac{1}{\pi} \cdot \frac{1}{1+x^{2}} \end{align*} \]

Das ist die Dichtefunktion der standardisierten Cauchy-Verteilung

\[ f_{(\mu,\lambda)}(x) = \frac{1}{\pi} \cdot \frac{\lambda}{\lambda^2+(x-\mu)^2} \]

mit (\(\mu = 0\) und \(\lambda=1\)), welche – bekanntermaßen – keinen Erwartungwert hat.

Wegen

\[ \begin{align*} \lim_{x \to +\infty} \frac{f_1(k \cdot x)}{f_1(x)} &= \lim_{x \to +\infty} \frac{\frac{1}{\pi} \cdot \frac{1}{1+(kx)^{2}}}{\frac{1}{\pi} \cdot \frac{1}{1+x^{2}}} = \lim_{x \to +\infty} \frac{1+x^2}{1+k^2x^2} \\ &=\lim_{x \to +\infty} \frac{\frac{1}{x^2}+\frac{x^2}{x^2}}{\frac{1}{x^2}+k^2\frac{x^2}{x^2}} =\frac{1}{k^2}=k^{-2} \end{align*} \]

für alle reellen \(k>0\) ist \(f_1(x)\) eine regulär variierende Funktion mit Variationsindex \(\rho = -2\).

Die Überlebensfunktion zur t-Verteilung mit einem Freiheitsgrad lautet nun:

\[ \overline{F}_1(x) = \int_x^\infty f_1(t) \operatorname{d}t = \frac{1}{\pi} \cdot \int_x^\infty \frac{1}{1+x^{2}} \operatorname{d}t = \frac{\arctan(x)}{\pi} \]

da wir das optionale \(+C\) mit \(C=0\) annehmen dürfen.

Es gilt nun:

\[ \arctan`(x)= \frac{1}{1+x^2} \to \frac{1}{x^2} \text{ für } x\to \infty \]

Genauer gilt wegen

\[ \lim\limits_{x \to \infty} \frac{\frac{1}{1+x^2}}{\frac{1}{x^2}} = \lim\limits_{x \to \infty} \frac{x^2}{1+x^2} =1, \] dass \(\frac{1}{1+x^2} \sim \frac{1}{x^2}\), also asymptotisch äquivalent sind und somit auch \(\log\left(\frac{1}{1+x^2}\right) \sim \log\left(\frac{1}{x^2}\right)\).

Zusammen gefasst gilt somit: \[ \log\left(\frac{1}{\pi} \cdot \frac{1}{1+x^{2}}\right) \to -2\log(x) - \log(\pi) \text{ für } x \to \infty \]

Sei \(f_1^*(x) = C \cdot x^{-\alpha}\) mit \(\alpha = 2\) und \(C=\frac{1}{\pi} \approx0.3183\).

Schauen wir uns das einmal als Grafik an:

lower_bound <- 2
upper_bound <- 100
dfree <- 1

f_star <- function(x) {
  alpha <- 2
  C <- 1/pi
  C * x**(-alpha)
}

x <- seq(lower_bound, upper_bound, 0.1)

gf_dist("t", df = dfree, 
        xlim = c(lower_bound, upper_bound), 
        color = "darkred") %>%
  gf_line(f_star(x) ~ x, 
          color = "darkgreen")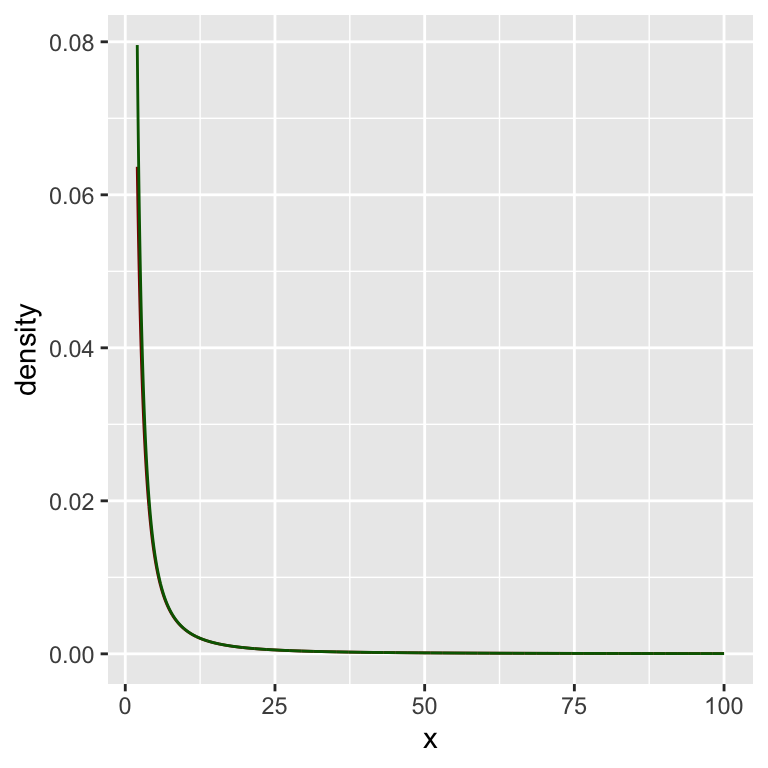

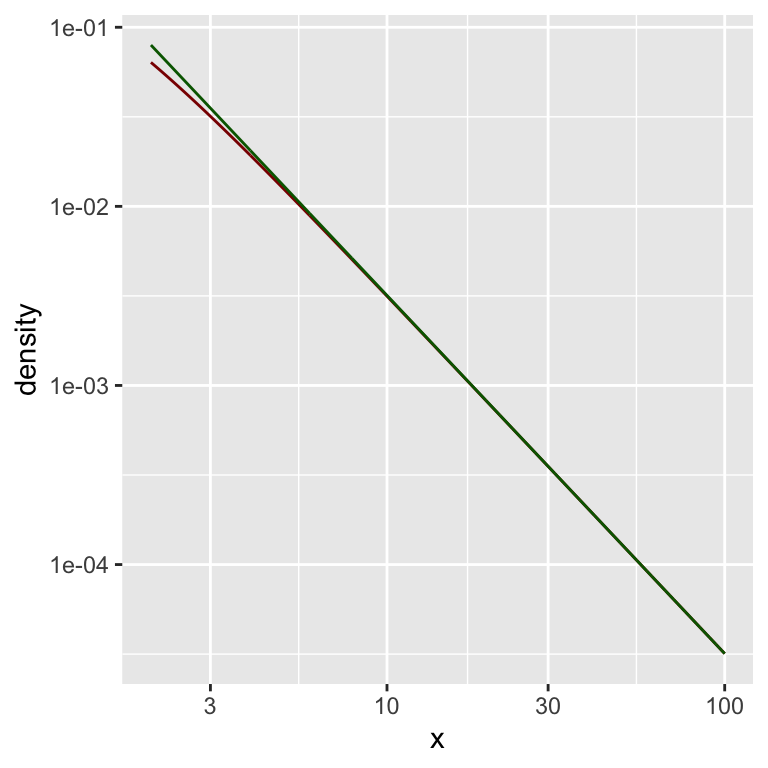
Hier eine doppelt-logarithmische Darstellung:

gf_dist("t", df = dfree, 
        xlim = c(lower_bound, upper_bound), 
        color = "darkred") %>%
  gf_line( f_star(x) ~ x, 
           color = "darkgreen") %>%
  gf_refine(
    scale_x_log10(),
    scale_y_log10()
  )

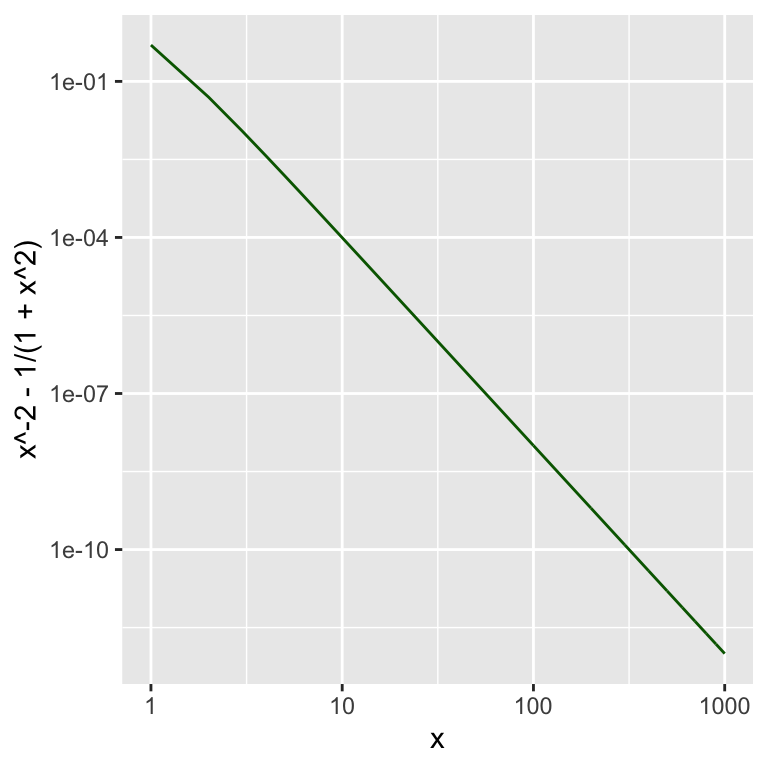
Wie groß ist nun der (absolute) Fehler zwischen \(f_1^*\) und \(f_1\)?

Eine Grafik von \(f_1^*-f_1\) zeigt:

x <- seq(1,1000,1)
  gf_line(x**-2 - 1/(1+x**2) ~ x, 
           color = "darkgreen") %>%
  gf_refine(
    scale_x_log10(),
    scale_y_log10()
  )

Genauer gilt:

\[ f_1^*(x) - f_1(x) = \frac{1}{x^2+x^4} \]

Wir können also für ein hinreichend großes \(x >> 1\) statt \(f_1\) auch \(f_1^*\) verwenden und erhalten somit:

\[ \begin{align*} \overline{F}_1(x) &\approx \int_x^\infty f_1^*(t) \operatorname{d}t = \int_x^\infty C \cdot t^{-\alpha} \operatorname{d}t \\ &= \frac{1}{\pi} \cdot \int_x^\infty t^{-2} \operatorname{d}t = \frac{1}{\pi}\left[\lim\limits_{\epsilon \to \infty} \left(-\epsilon^{-1}\right) -\left(-x^{-1}\right)\right]\\ &= \frac{1}{\pi}\cdot\left[0 + \frac{1}{x}\right] = \frac{1}{\pi \cdot x} \end{align*} \]

Wie hinreichend ist hier hinreichend groß?

Taleb schreibt an dieser Stelle gerne, dass man jenseits des Karamata-Punktes die Karamata-Konstante anwenden kann. Beides Begriffe, die keine echte Definition haben und ausserhalb der Sphäre von Taleb auch kaum Verwendung finden.

Die Karamata-Konstante ist \(\rho = -\alpha\).

Der Karamata-Punkt bleibt nebulös. Vermutlich könnte man hier so argumentieren:

Wenn die Fehler zwischen \(f\) und \(f^*\) hinreichend klein ist.

Hierfür könnte man einen absoluten Fehler oder einen relativen Fehler als Maßstab ansehen.

Für einen relativen Fehler vielleicht \(\frac{f^*-f}{x} < k\)?

Oder man betrachtet hier gleich \(\frac{f^*-f}{\log(x)} < k^*\)?

t-Verteilung mit zwei Freiheitsgeraden

Für \(f_2(x)\) ergibt sich somit:

\[ \begin{align*} f_2(x) &= \frac{\Gamma\left(\frac{n+1}{2}\right)} {\sqrt{n\pi}~\Gamma\left(\frac{n}{2}\right)}\left(1+\frac{x^{2}}{n}\right)^{-\frac{n+1}{2}} \\ &= \frac{\Gamma\left(\frac{3}{2}\right)} {\sqrt{2\pi}~\Gamma\left(\frac{2}{2}\right)}\left(1+\frac{x^{2}}{2}\right)^{-\frac{3}{2}} \\ &= \frac{\Gamma\left(\frac{3}{2}\right)} {\sqrt{2\pi}~\Gamma\left(1\right)}\left(1+\frac{x^{2}}{2}\right)^{-\frac{3}{2}} \\ \end{align*} \]

Wegen \(\Gamma(1) = 0! = 1\) und \(\Gamma\left(\frac{3}{2}\right)=\frac{\sqrt{\pi}}{2}\) ergibt sich nun:

\[ \begin{align*} f_2(x) &= \frac{1}{2\sqrt{2}} \cdot \left(1+\frac{x^{2}}{2}\right)^{-\frac{3}{2}} \\ &= \frac{1}{\sqrt[2]{2^3} \cdot \sqrt[2]{\left(1+\frac{x^{2}}{2}\right)^3}} \\ &= \frac{1}{(x^2+2)^{\frac{3}{2}}} \\ &= \frac{1}{\sqrt{(x^2+2)^3}} \end{align*} \]

Wegen

\[ \begin{align*} \lim_{x \to +\infty} \frac{f_2(k \cdot x)}{f_2(x)} &= \lim_{x \to +\infty} \frac{\frac{1}{\sqrt{((k\cdot x)^2+2)^3}}}{\frac{1}{\sqrt{(x^2+2)^3}}} = \lim_{x \to +\infty} \frac{\sqrt{(x^2+2)^3}}{\sqrt{((k\cdot x)^2+2)^3}} \\ &= \lim_{x \to +\infty} \left(\frac{x^2+2}{k^2x^2+2}\right)^\frac{3}{2}=\lim_{x \to +\infty} \left(\frac{\frac{x^2}{x^2}+\frac{2}{x^2}}{k^2\frac{x^2}{x^2}+\frac{2}{x^2}}\right)^\frac{3}{2} \\ &=\left(\frac{1}{k^2}\right)^\frac{3}{2}=\frac{1}{k^3}=k^{-3} \end{align*} \]

für alle reellen \(k>0\) ist \(f_2(x)\) eine regulär variierende Funktion mit Variationsindex \(\rho = -3\).

Die Überlebensfunktion zur t-Verteilung mit einem Freiheitsgrad lautet nun:

\[ \begin{align*} \overline{F}_2(x) &= \int_x^\infty f_2(t) \operatorname{d}t = \int_x^\infty \frac{1}{\sqrt{(t^2+2)^3}} \operatorname{d}t \\ &= \frac{x}{2 \cdot \sqrt{x^2+2}} \end{align*} \]

da wir das optionale \(+C\) mit \(C=0\) annehmen dürfen.

Es gilt für jedes feste \(k>0\):

\[ \begin{align*} \lim\limits_{x \to \infty} \frac{\overline{F}_2(k x)}{\overline{F}_2(x)} &= \lim\limits_{x \to \infty}k \cdot \sqrt{\frac{x^2+2}{k^2x^2+2}} \\ &= k \cdot \lim\limits_{x \to \infty} \sqrt{\frac{1}{k^2} \cdot \frac{x^2+2}{x^2+\frac{2}{k^2}}} \\ &= \frac{k}{k} \cdot \lim\limits_{x \to \infty} \sqrt{ \frac{x^2+2}{x^2+\frac{2}{k^2}}} = 1\end{align*} \]

Wegen

\[ \lim_{x \to \infty} \frac{\frac{1}{\sqrt{(x^2+2)^3}}}{\frac{1}{x^3}} =\lim\limits_{x \to \infty} \frac{x^3}{(\sqrt{x^2+2})^3} = \lim\limits_{x \to \infty} \left(\frac{x}{\sqrt{x^2+2}}\right)^3= 1 \]

ist \(f_2 \sim f^*_2\) und somit auch \(\log(f_2) \sim \log(f^*_2)\).

Aus \(\log\left(\frac{1}{x^3}\right) = \log(1)- 3\cdot\log(x)\) können wir daher auf \(\alpha = 3\) und \(C=1\) schliesse und schreiben:

\[ f_2^*(x) = C \cdot x^{-\alpha} = x^{-3} \]

Schauen wir uns das einmal als Grafik an:

lower_bound <- 2
upper_bound <- 100
dfree <- 2

f_star <- function(x) {
  alpha <- 3
  C <- 1
  C * x**(-alpha)
}

x <- seq(lower_bound, upper_bound, 0.1)

gf_dist("t", df = dfree, 
        xlim = c(lower_bound, upper_bound), 
        color = "darkred") %>%
  gf_line(f_star(x) ~ x, 
          color = "darkgreen")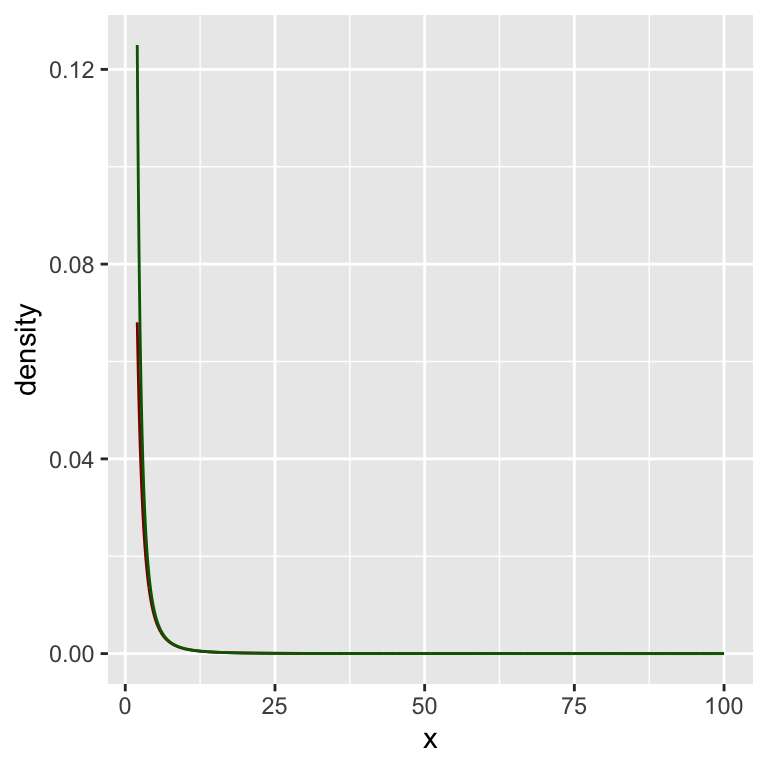

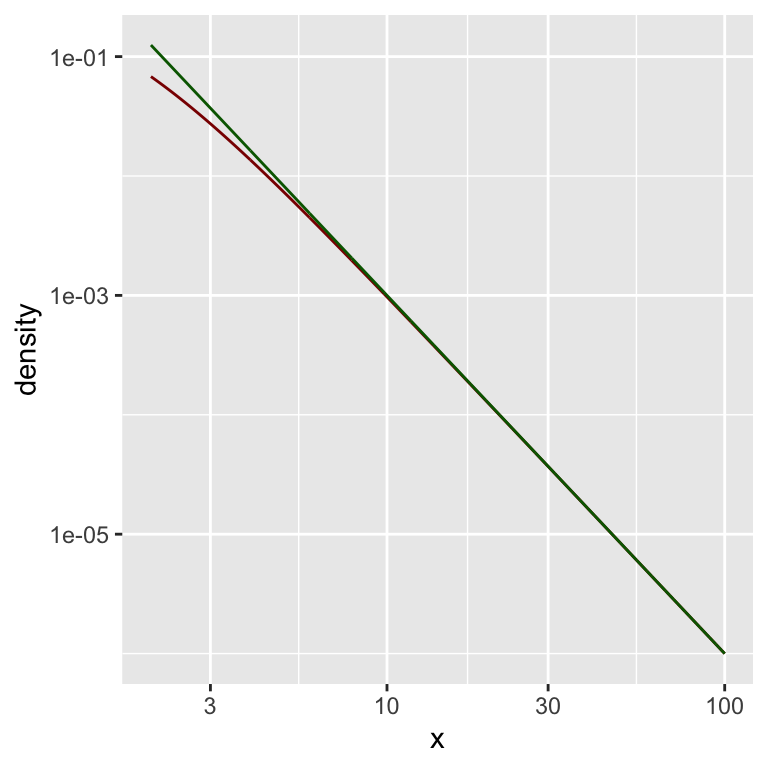
Hier eine doppelt-logarithmische Darstellung:

gf_dist("t", df = dfree, 
        xlim = c(lower_bound, upper_bound), 
        color = "darkred") %>%
  gf_line( f_star(x) ~ x, 
           color = "darkgreen") %>%
  gf_refine(
    scale_x_log10(),
    scale_y_log10()
  )

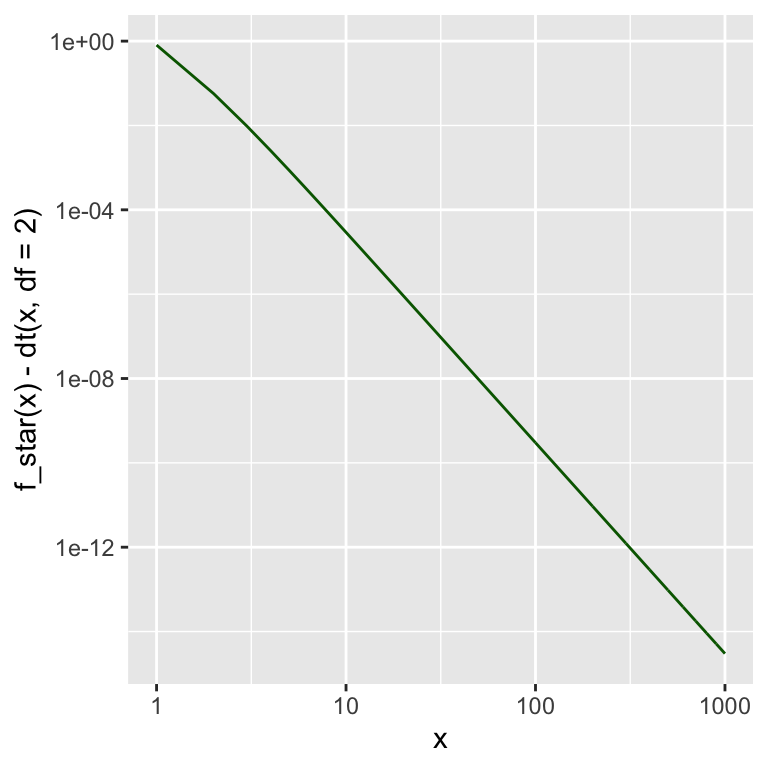
Wie groß ist nun der absolute Fehler zwischen \(f_2^*\) und \(f_2\) genau?

Eine Grafik zeigt von \(f_2^*-2_1\) zeigt:

x <- seq(1,1000,1)
  gf_line(f_star(x) - dt(x,df=2) ~ x, 
           color = "darkgreen") %>%
  gf_refine(
    scale_x_log10(),
    scale_y_log10()
  )

Fussnoten