Histogramme und Hypothesen

Exkurs: Warum Histogramme, die 10000 wiederholten Stichproben und dieser Wert bei 9500?

Mir ist bei der Nachbereitung der Vorlesung aufgefallen, dass einige von Ihnen noch nicht so ganz wissen, wieso wir eine Zeile wie

Simulation <- do(10000)*mean(rnorm(n=200, mean=100, sd=50))

schreiben, kurz, wieso wir simulieren und vor allem was wir simulieren und wie das ganze nun mit den Hypothesentests zusammenhängt. Ich will mit diesem vorangestelltem Exkurs versuchen die Fragen zu klären.

Schauen wir zunächst darauf was wir mit den R-Zeilen genau bewirken:

Mit dem Stück

rnorm(n=200, mean=100, sd=50)

erhalten wir (n=)200 Zufallszahlen, die normalverteilt mit dem Mittelwert (mean=)100 und der Standardabweichung (sd=)50 sind.

Die 200 Zufallszahlen werden nun mit mean() zu einem Mittelwert zusammengefasst. Da es 200 zufällige Zahlen sind, die der theoretischen Verteilung (Normalvertieung mit \(\mu=100\) und \(\sigma=50\)) gehorchen sollten, können wir nicht davon ausgehen, dass das arithmetische Mittel tatsächlich 100 ist. Das Gesetz der großen Zahlen sagt uns nur, dass wenn wir n sehr groß wählen würden, das arithmetische Mittel immer näher an theoretischen Mittelwert \(\mu=100\) herran reichen würde. Die Abweichungen unserer Stichproben sind aber nicht schädlich, sondern genau die wollen wir hier haben! Wir stellen uns nämlich die theoretische Verteilung, also die Normalverteilung zu den Parametern \(\mu=100\) und \(\sigma=50\), als unsere Grundgesamtheit vor und ziehen daraus eine Stichprobe vom Umfang 200. Und betrachten dann den Mittelwert:

mean(rnorm(n=200, mean=100, sd=50))

## [1] 104.2809

Diesen Vorgang wiederholen wir nun 10.000 mal um 10.000 solcher Mittelwerte zu erhalten, die alle jeweils eine Stichprobe vom Umfang 200 aus der gedachten Normalverteilung sind. Da jede dieser Stichproben zufällig ist, sollten die sich insgesamt genauso verhalten, wie die Verteilung der Grundgesamtheit, also der Normalverteilung, es vorherbestimmt.

Genau das machen wir mit

Simulation <- do(10000)*mean(rnorm(n=200, mean=100, sd=50))

Um zu Prüfen, bzw. um zu sehen, wie gut diese Näherung ist, schauen wir uns das Histogramm an:

Der schnelle Weg ist dabei die folgende Zeile:

hist(Simulation$mean)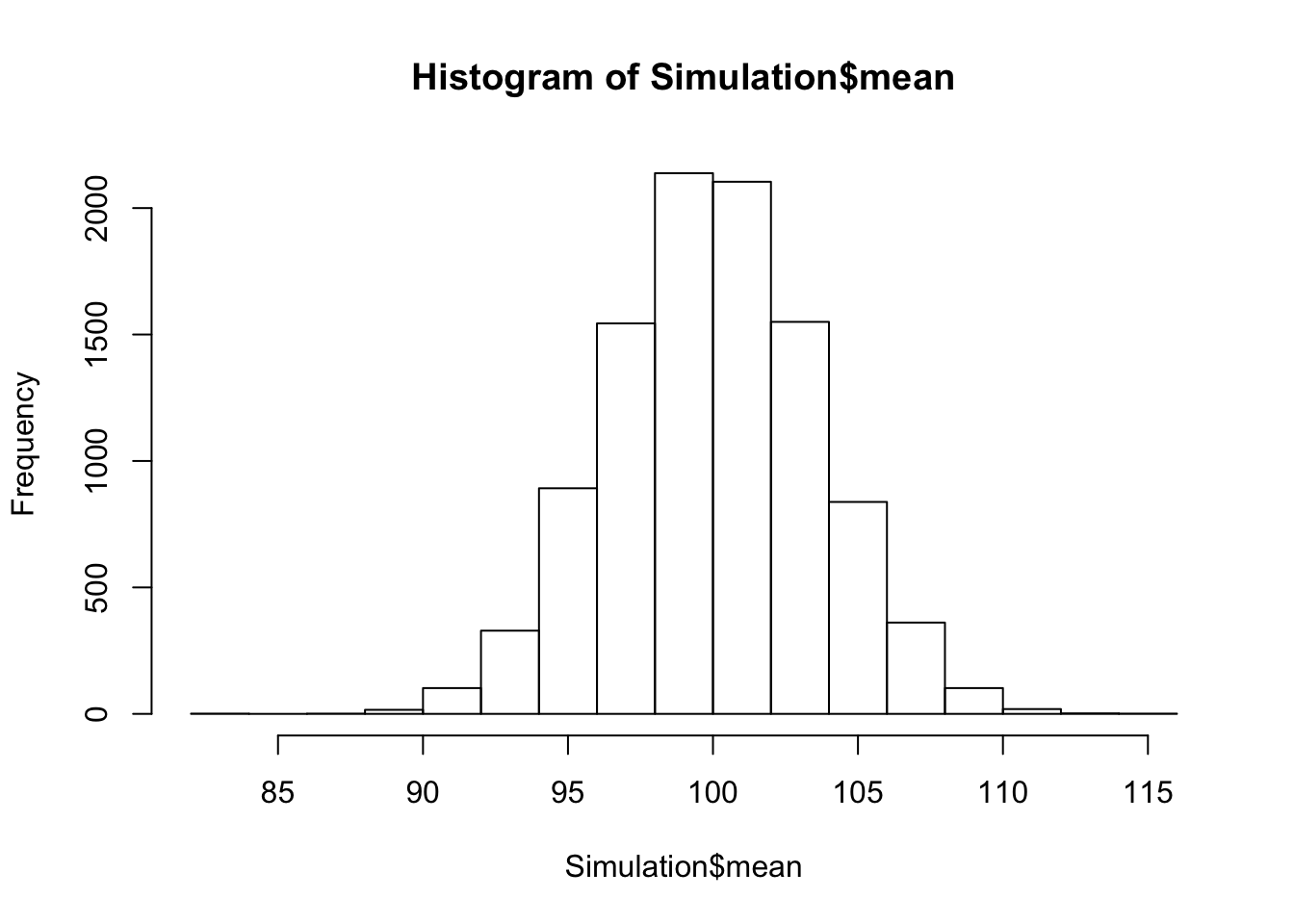

Um aber alles etwas feiner augelöst zu haben fügen wir die Anzahl der breaks mit ein:

hist(Simulation$mean, breaks=30)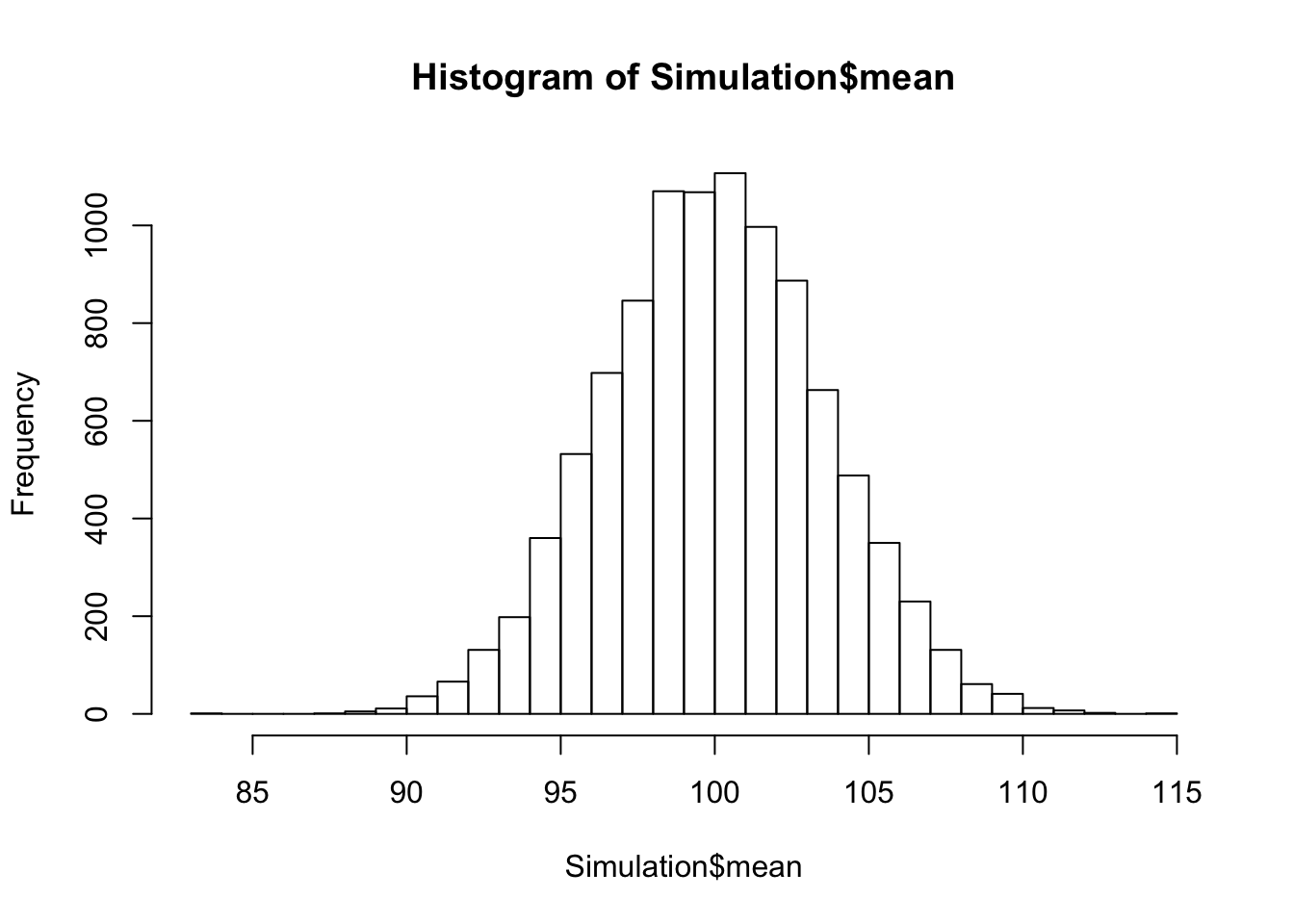

Auf der linken Achse sehen sie die Beschriftung Freqency, also die Anzahl der Mittelwerte pro Balken. Was wir dort lieber hätten wäre die Dichte, also Density. Daher ändern wir die Zeile ab:

hist(Simulation$mean, freq=FALSE, breaks=30)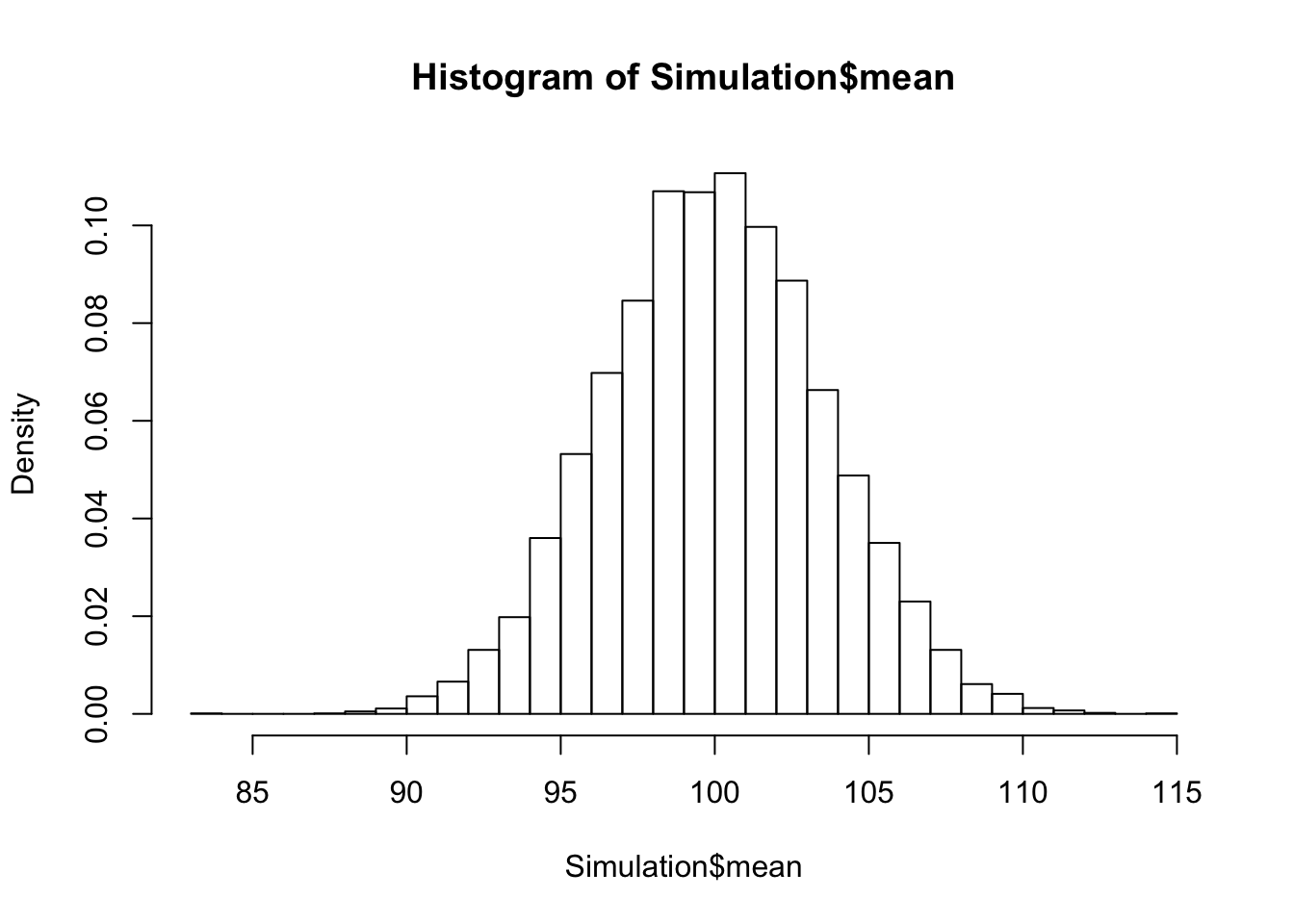

Sie sehen, es hat sich nur die Beschriftung geändert!

Passen wir nun noch den Bereich auf den für uns interessanten Bereich von 80 bis 120 und auch die Höhen an:

hist(Simulation$mean, freq=FALSE, breaks=30, xlim=c(80,120), ylim=c(0,0.12))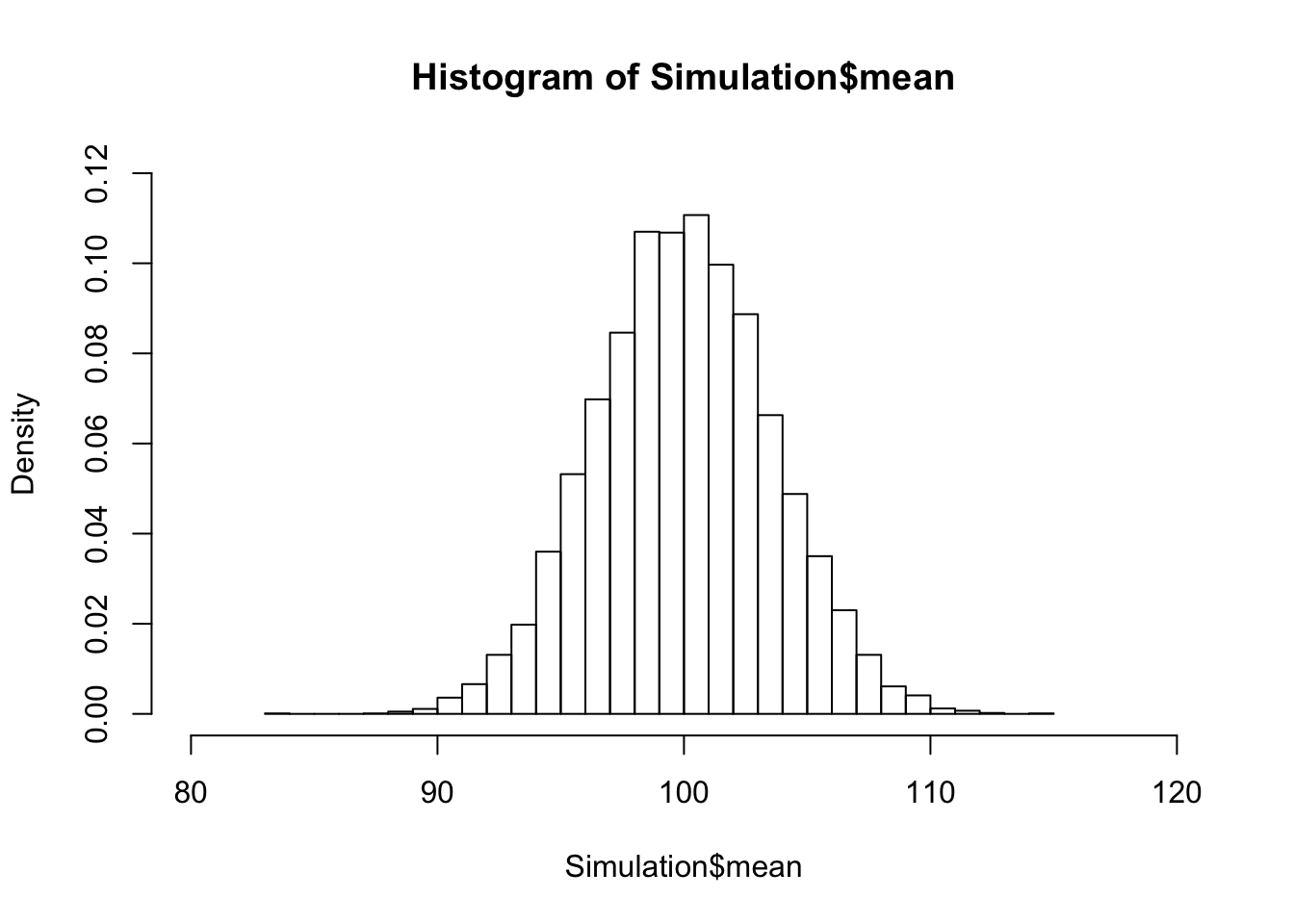

Machen wir uns noch etwas mehr Arbeit (mit ggplot2), dann haben wir, zum besseren Verständnis, folgenden Plot:

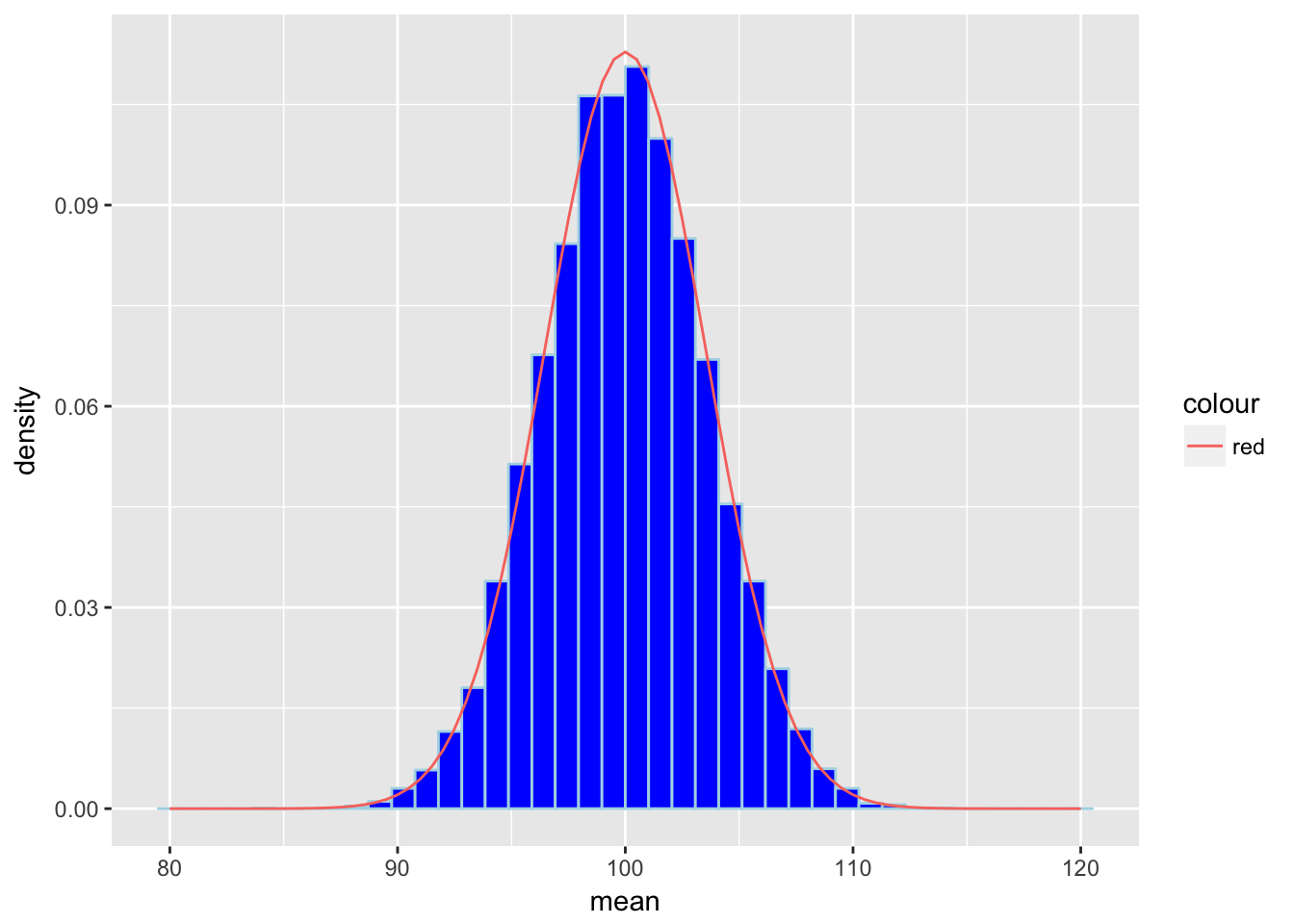
Die blauen Balken sind unsere Mittelwerte. Diese sind jeweils gruppiert, also zusammengefasst, so das wir insgesamt Balken haben.

Die rote Linie ist die zugehörige Dichtefunktion der theoretischen Verteilung.

Sie sehen also, dass unsere Balken sich in etwa so verhalten, wie die Dichtefunktion. Wenn wir unsere Mittelwerte sortieren, haben wir damit eine gute Näherung zu des benötigten Quantils. Dazu brauchen wir nun noch an der richtgien Stelle nachsehen. Die Quantile sind entscheidenden kritschen Werte in unseren Hypothesentests. Sie entscheiden darüber, zusammen mit dem Ergebinis des Stichprobe (und diese ist NICHT unsere Simulation!), ob wir \(H_0\) ablehnen oder nicht.

Noch einmal: Wir nutzen unsere Simulation dafür den kritischen Wert resp. das 95%-Quantil für unsere Hypothesentests zu ermitteln!

Sortieren wir unsere Simulationsdaten zunächst mit:

library(dplyr)
SimSorted <- arrange(Simulation, mean) 

Das verändert die Qualität unserer Näherung nicht. Denn wie sie sehen, ist die Stuktur der Histogramme gleich geblieben:

hist(Simulation$mean, freq=FALSE)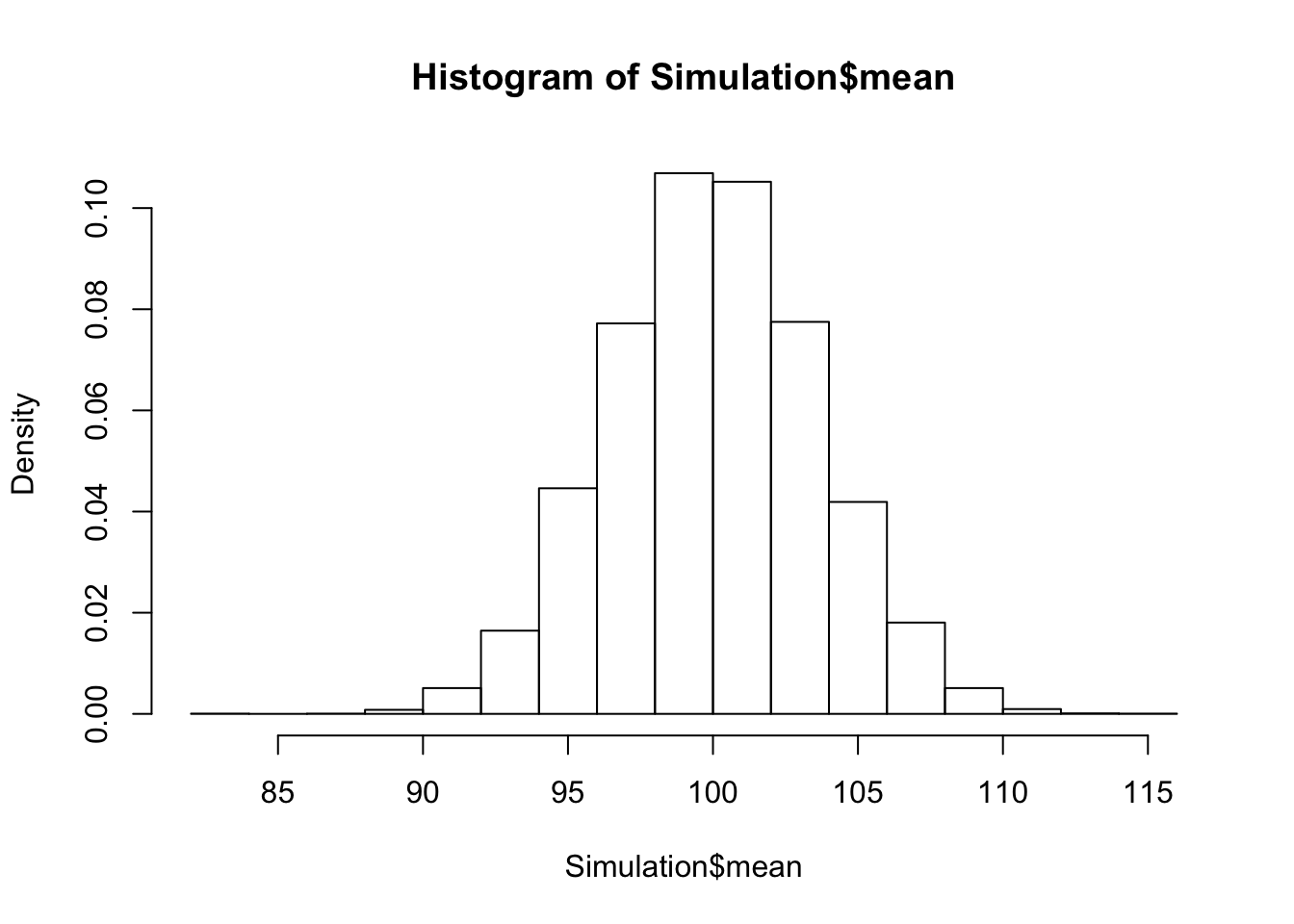

bzw.

hist(SimSorted$mean, freq=FALSE)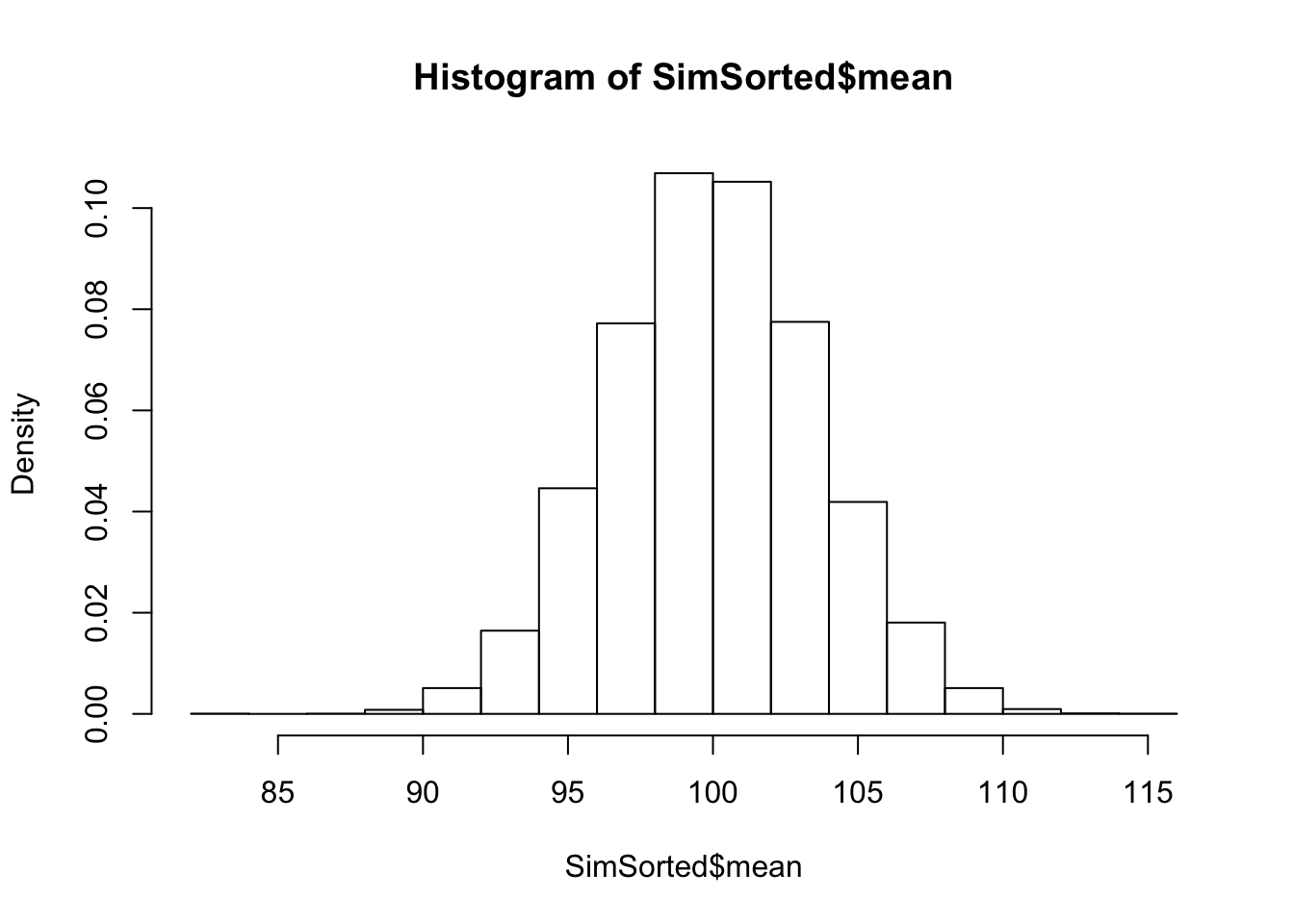

Durch das sortieren können wir aber das 95%-Quantil einfacher ‘bestimmen’! Unsere Datengrundlage in der Simulation waren 10^{4} Mittelwerte. Wenn wir nun das 95%-Quantil bestimmen wollen, damit wir die oberen 5%, also unseren \(\alpha\)-Bereich abgrenzen können, dann brauchen wir nur nach dem 9500-ten Element in der Mittelwertsliste zu suchen:

SimSorted$mean[9500]

## [1] 105.9454

Für Anhönger von dplry und pipes:

SimSorted %>%
filter(mean, row_number()==9500)

##       mean
## 1 105.9454

Dieses Vorgehen dient nur der Verdeutlichung!

Eigentlich kann man den Quantilswert mit R sehr einfach berechnen lassen. Die Simulation wäre also eigentlich nicht nötig! Der theoretische Wert liegt bei:

qnorm(0.95, mean=100, sd=50/sqrt(200))

## [1] 105.8154

Oh, ist Ihnen etwas aufgefallen? Da steht doch glatt sd=50/sqrt(200) und nicht, wie sie vielleicht vermutet haben, sd=50!

Das Geheimnis ist zugleich ein Grund für unseren Weg der Berechnung der Quantile über die Simulation. Folgt man unserem Weg mit der Simulation, brauchen wir nicht viel machen und wir nähern uns dem gesuchten Quantil quasi kanonisch.

Will man den Wert aber berechnen, dann sind Anpassungen nötig!

Dahinter steckt im Wesendlichen das sogenannte \(\sqrt{n}\)-Gesetz:

Seien \(X_1, \cdots, X_n\) Zufallsvariablen mit gleichem Mittelwert \(\mu\) und gleicher Varianz \(\sigma\), dann gilt die für Summe \(S_n= \sum X_i\) aller \(n\) Zufallsvariablen:

\[ E(S_n) = \mu \qquad \text{ und } \qquad Var(S_n) = \frac{\sigma^2}{n} \]

Für die Standardabweichung, welche ja die Wurzel der Varianz ist, bedeutet das nun \[ \sigma_{S_n} = \frac{\sigma}{\sqrt{n}}, \] was den Namen des Gesetzes und auch unsere Anpassung erklärt.

“Der” FOM-Student hat im Mittel 300 Facebook-Freunde!

Wir laden die Daten direkt aus dem Internet:

extra <- read.csv(
    "https://raw.githubusercontent.com/sebastiansauer/Daten_Unterricht/master/extra.csv")

Der Mittelwert der Facebookfreunde kann nicht ohne weiteres berechnet werde:

mean(extra$n_facebook_friends)

## [1] NA

Aber wenn wir die fehlenden Werte herausnehmen, dann geht es:

mean(extra$n_facebook_friends, na.tm=TRUE)

## [1] NA

Wir simulieren nun die Situation:

library(mosaic)
library(dplyr)
simulation <- do(10000)*mean(rnorm(n=1000, mean=300, sd=100))

Und geben nun das Histogramm dazu aus:

hist(simulation$mean)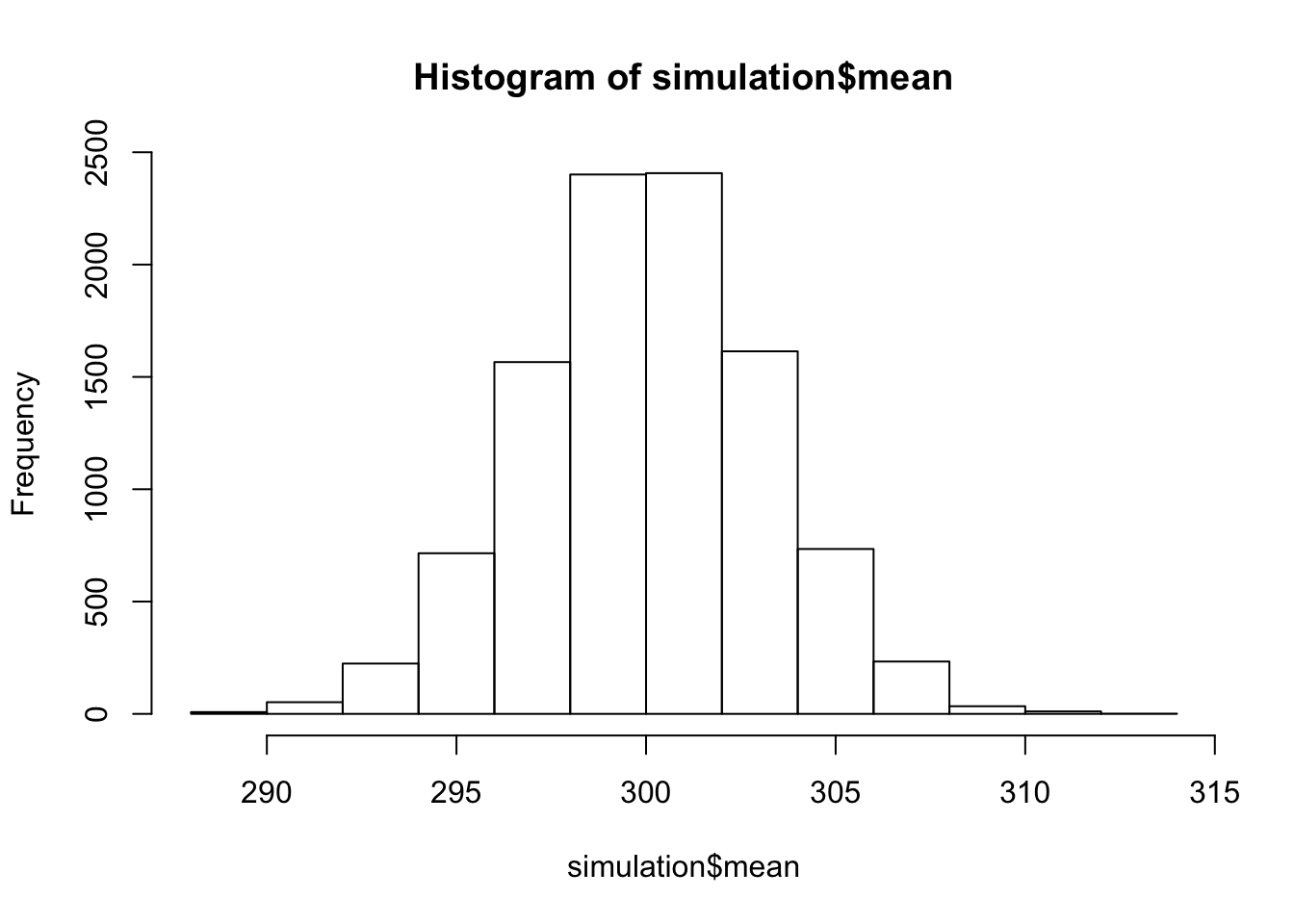

Wir sortieren kurz unsere Simulatiom

library(dplyr)
df <- arrange(simulation, mean)

Und suchen den p-Wert für ein Signifikanzniveau von 5%

df$mean[9500]

## [1] 305.131

Oh je, das liegt deutlich unter dem Mittelwert unserer Stichprobe:

mean(extra$n_facebook_friends, na.tm=TRUE)

## [1] NA

Also \(H_0\) ablehnen … “Der” FOM-Student hat also mehr als nur 300 FB-Freunde!

Mittlerer Mietpreis am Münchner Wohnungsmarkt

Formulieren wir zu Beginn unseren Hypothesentest:

\(H_0\): \(\mu = \mu_0 = 16{,}28\) (bei \(\sigma=2\))- Der mittlere Mietpreis beträgt 16,28€!

\(H_A\): \(\mu \geq \mu_0\) bei \(\sigma=2\) - Der mittlere Mietpreis liegt höher!

Wir prüfen mit einem Signifikanzniveau von \(\alpha=5\%=0{,}05\)!

Dazu ziehen wir jeweils n=16 (simulierte) Stichproben:

Miete_H0_MW <- 16.28
Miete_H0_SD <- 2
Miete_X_MW <- 18.10

Miete_n <- 16
Miete_alpha <- 0.05
Sim_n <- 10000
MieteSim <- do(Sim_n)*mean(rnorm(n=Miete_n, mean=Miete_H0_MW, sd=Miete_H0_SD))
MieteSimSort <- arrange(MieteSim, mean)
kritWertSim <- MieteSimSort$mean[Sim_n*(1-Miete_alpha)]

Der kritische Wert der Simulation ist:

kritWertSim

## [1] 17.11422

Schauen wir nun ob wir \(H_0\) verwerfen können? (vgl. Seite 214 im Skript!) (Einseitiger Test “rechts”):

Miete_X_MW > kritWertSim

## [1] TRUE

Wir können also bei TRUE unsere Hypothese \(H_0\) ablehnen (und müssten bei FALSE \(H_1\) verwerfen).

Alternativ können wir auch einen anderen Weg gehen:

Wir führen zunächst eine z-Transformation durch! Wir übertragen also unser Problem in die Welt der Standardnormalverteilung: \[ z = \frac{\bar{X}-\mu}{SE} = \frac{\delta}{\frac{\sigma}{\sqrt{n}}} \] In R geht das wir folgt:

# Erst zentrieren:
delta <- Miete_X_MW - Miete_H0_MW
SE <- Miete_H0_SD / sqrt(Miete_n)
z <- delta/ SE

Der z-Wert lautet dann:

z

## [1] 3.64

Der zu \(z\) gehörende \(p-Wert\) lautet:

p <- 1 - pnorm(z)
p

## [1] 0.000136319

Wiegt dieser Wert nun unterhalt unseres Signifikanzniveaus \(\alpha\), so lehnen wir \(H_0\) ab:

p < Miete_alpha

## [1] TRUE

Wir haben also das selbe Ergebnis, jedoch auch einen p-Wert ermittelt

Noch eine Alternative

Wie in der Einleitung beschrieben, gibt es noch einen kürzeren Weg für (Semi-)Profis:

xp <- qnorm(1-Miete_alpha, mean=Miete_H0_MW, sd=Miete_H0_SD / sqrt(Miete_n))
xp

## [1] 17.10243

Miete_X_MW > xp

## [1] TRUE

Moment mal? - Wieso denn schon wieder nur “Semi-Profi”. - Nun, das werden Sie verstehen, wenn wir den t-Test in der Vorlesung behandeln.

Denn eigentlich haben wir ein Problem: Wie kommt man auf die Standardabweichung des Modells?

Bisher haben wir die immer als gegeben vorausgesetzt. In der Realität ist aber dieser Wert alles andere als natürlich gegeben! Und genau die Schätzung dieses Wertes macht leider einige Modifikationen notwendig… Dazu später mehr!