Die Geschichte der Newcomb-Benford-Analyse
Nach Wikipedia wurde das Newcomb-Benford-Gesetz (im engl. oft mit NBL für “Newcomb-Benford’s Law” abgekürzt) schon 1881 vom Astronomen und Mathematiker Simon Newcomb entdeckt und im American Journal of Mathematics veröffentlicht. Aber erst im Jahre 1938 wurde sie vom Elektroingenieur und Physiker Frank Banford wiederentdeckt und erneut publiziert.
Bendford-Verteilung
Für eine gegebene Menge von Zahlen, welche dem NBL gehorchen, gilt für die Wahrscheinlichkeit des Auftretens der Ziffer \(d\) zur Basis \(B\) an der \(n\)-ten Stelle (gezählt von vorne und mit 0 startend):
\[p_n(d) = \sum_{k = \lfloor B^{n-1}\rfloor}^{B^n-1} \log_B\left(1+ \frac{1}{k \cdot B + d}\right)\] wobei \(\lfloor . \rfloor\) die Gaußklammer ist.
Die Gaußklammer entspricht dem “Abrunden”:
\[\lfloor x \rfloor :=\max \{k\in\mathbb{Z} \mid k\leq x\}\]
Betrachtet man nur die erste Ziffer (\(n=0\)) so können wir die Formeln etwas vereinfachen:
\[p(d) = p_0(d) = \log_B \left( 1 + \frac{1}{d} \right) = \log_B \left(\frac{d+1}{d} \right) = \log_B(d+1) - \log_B(d)\]
Für Dezimalzahlen (\(B=10\)) tritt dann die Ziffer \(d\) an der ersten Stelle mit der Wahrscheinlichkeit \[p(d) = \log_{10}(d+1)-\log_{10}(d)\] auf. Wir erhalten damit:
library(tidyverse)
benford.simple <- function(d) {
return(log10(d+1)-log10(d))
}
benford.tab <-sapply(1:9, benford.simple)
benford.df <- data_frame(x=1:9, y=benford.tab*100)
colnames(benford.df) <- c("Führende Ziffer", "Wahrscheinlichkeit")
knitr::kable(benford.df,
digits = 2,
format.args = list(decimal.mark = ","),
caption = "NBL für die erste Ziffer. Wahrscheinlichkeiten in Prozent")| Führende Ziffer | Wahrscheinlichkeit |
|---|---|
| 1 | 30,10 |
| 2 | 17,61 |
| 3 | 12,49 |
| 4 | 9,69 |
| 5 | 7,92 |
| 6 | 6,69 |
| 7 | 5,80 |
| 8 | 5,12 |
| 9 | 4,58 |
Schauen wir uns nun das Dataframe Objekt einmal als Grafik an:
ggplot(benford.df) +
geom_col(aes(x = `Führende Ziffer`, y = Wahrscheinlichkeit)) +
scale_x_continuous(breaks = 1:9)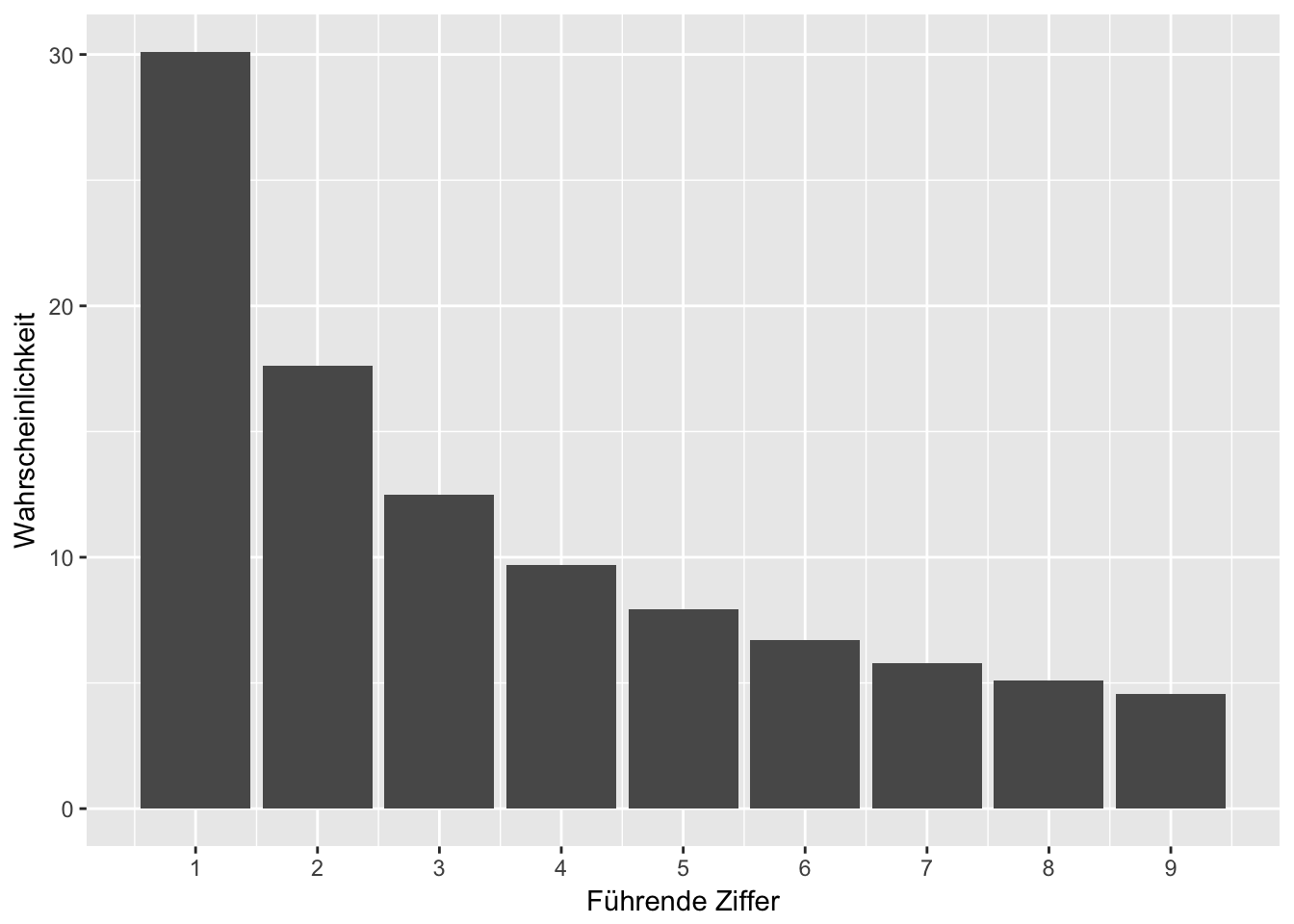
Diese neun Balken zeigen die Verteilung der Ziffernhäufigkeit nach dem Newcomb-Benfordschen Gesetz, diese Verteilung ist unsere Erwartungshaltung an andere nummerische Datenbestände, wenn diese einem natürlichen Wachstum unterliegen.
Analyse der Verteilung der ersten Ziffer in Zahlungsdaten
Jetzt brauchen wir Daten mit nummerischen Beträgen, die wir nach Newcomb-Benford testen möchten. Für dieses Beispiel nehme wir aus einem einem SAP-Testdatensatz die Spalte ‘DMBTR’ der Tabelle ‘BSEG’ (SAP FI). Die Spalte ‘DMBTR’ steht für “Betrag in Hauswährung’, die ‘BSEG’ ist die Tabelle für die buchhalterischen Belegsegmente. Die Datei mit den Testdaten ist über diesen Link zum Download verfügbar (Klick) und enthält 40.000 Beträge.
Wir laden diese Daten nun direkt in R:
library(readr)
financialTransactions <- read_csv("https://data-science-blog.com/download/BSEG_DMBTR.csv")## Parsed with column specification:
## cols(
## DMBTR = col_double()
## )colnames(financialTransactions) <- c("Zahlungen")
glimpse(financialTransactions)## Observations: 40,000
## Variables: 1
## $ Zahlungen <dbl> 2.01, 97.76, 7.30, 1.83, 0.16, 15.61, 2.55, 0.64, 0....firstDigit <- function(x) {
y <- abs(x)
return (substring( format(y, scientific = TRUE), 1, 1))
}
benford.data <- sapply(financialTransactions$Zahlungen, firstDigit)
benford.tab2 <- prop.table(as.numeric(table(benford.data)))
benford.df2 <- data_frame(x=1:9, y=benford.tab2*100)
colnames(benford.df2) <- c("Führende Ziffer", "Häufigkeit")
knitr::kable(benford.df2,
digits = 2,
format.args = list(decimal.mark = ","),
caption = "NBL für die erste Ziffer. Häufigkeiten in Prozent")| Führende Ziffer | Häufigkeit |
|---|---|
| 1 | 29,73 |
| 2 | 17,42 |
| 3 | 12,41 |
| 4 | 9,86 |
| 5 | 7,53 |
| 6 | 7,17 |
| 7 | 5,59 |
| 8 | 5,14 |
| 9 | 5,14 |
Abgleich der Ziffernhäufigkeit mit der Erwartung nach dem NBL
Nun bringen wir die theoretische Verteilung der Ziffern und die tatsächliche Häufigkeiten der ersten Ziffern in unseren Zahlungsdaten in einem Plot zusammen:
#benford.df3 <- merge(benford.df, benford.df2, by="Führende Ziffer")
full_join(benford.df, benford.df2, by="Führende Ziffer") %>%
gather("Type", "Prozent", c(2,3)) %>%
ggplot(aes(x = `Führende Ziffer`, y = Prozent, fill = Type)) +
geom_col(position = position_dodge(0.9)) +
scale_x_continuous(breaks = 1:9) +
scale_fill_hue(name="Quelle", h.start = 10, direction = -1,
breaks=c("Häufigkeit", "Wahrscheinlichkeit"),
labels=c("Finanzdaten", "Benford-Verteilung")) +
ggtitle("Vergleich der Benford-Verteilung mit den Finanzdaten")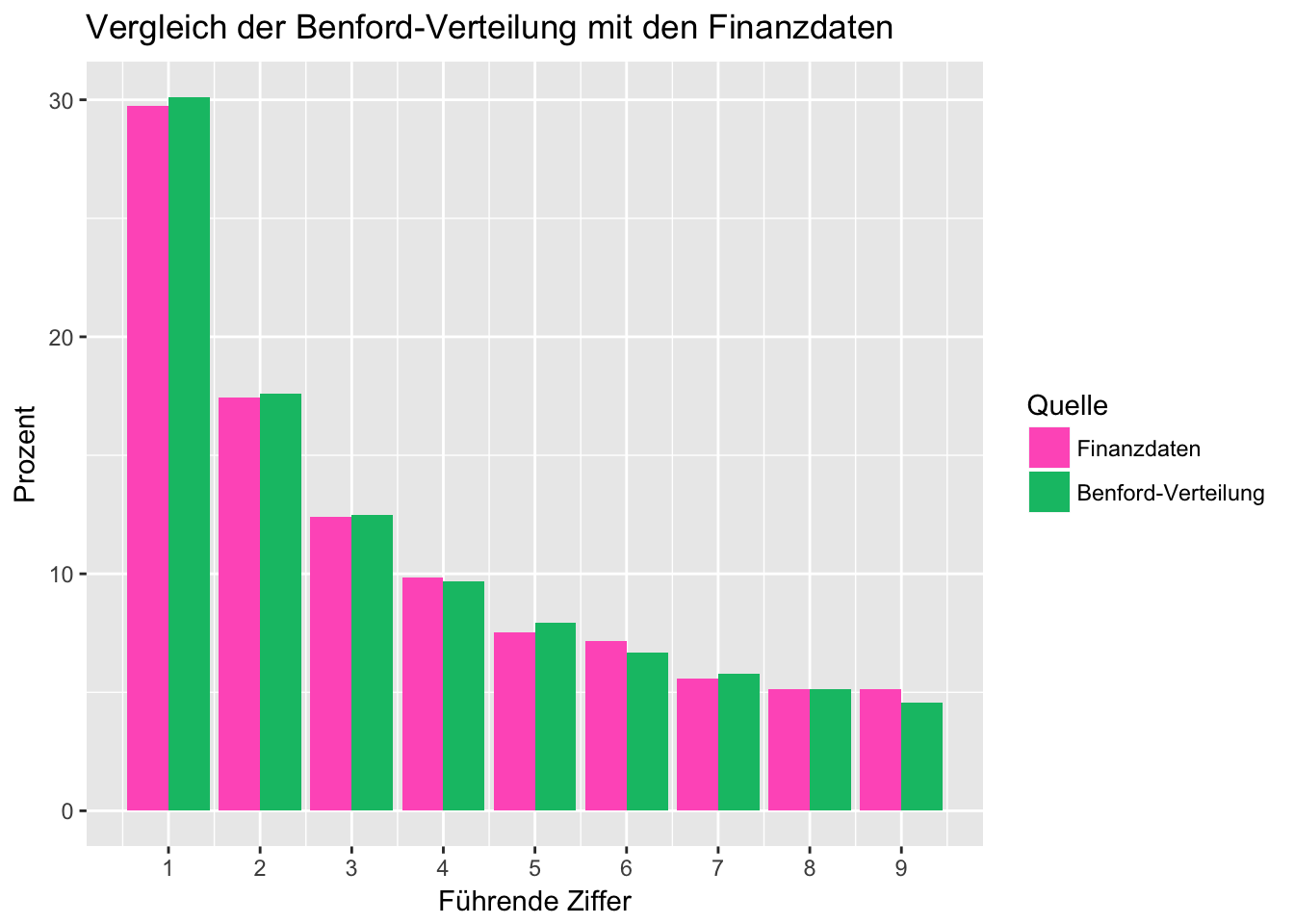
In dem Plot wird deutlich, dass die Häufigkeitsverteilung der führenden Ziffer in unseren Zahlungsdaten ziemlich genau unserer Erwartung nach dem Newcomb-Benfordschen Gesetz entspricht. Es sind keine außerordentlichen Ausreißer erkennbar. Das wäre auch absolut nicht zu erwarten gewesen, denn der Datensatz ist mit 40.000 Einträgen umfassend genug, um dieses Muster gut abbilden zu können.
Chi-Quadrat Test
benford.testtab <- full_join(benford.df, benford.df2, by="Führende Ziffer") %>%
mutate(Erwartet = Wahrscheinlichkeit * length(benford.data) /100 ) %>%
mutate(Tatsächlich = Häufigkeit * length(benford.data) /100 ) %>%
select(one_of(c('Tatsächlich', 'Erwartet')))
chisq.test(benford.testtab$`Tatsächlich`, # Gemessene Werte
p=benford.testtab$`Erwartet`, # Erwartete Werte
rescale.p = TRUE) # Angaben alle als absolute Häufigkeiten##
## Chi-squared test for given probabilities
##
## data: benford.testtab$Tatsächlich
## X-squared = 56.052, df = 8, p-value = 2.756e-09Es geht auch etwas direkter mit:
chisq.test(table(benford.data), # Gemessene Daten
p=benford.tab) # Benford-Verteiluungstabelle direkt##
## Chi-squared test for given probabilities
##
## data: table(benford.data)
## X-squared = 56.052, df = 8, p-value = 2.756e-09Ziffernweise Analyse
benford.df4 <- data_frame(
`Führende Ziffer` = 1:9,
`Wahrscheinlichkeit` = benford.tab,
`Häufigkeiten` = benford.tab2
)
xx <- chisq.test(benford.df4$Häufigkeiten, p=benford.df4$Wahrscheinlichkeit, rescale.p = T)## Warning in chisq.test(benford.df4$Häufigkeiten, p =
## benford.df4$Wahrscheinlichkeit, : Chi-squared approximation may be
## incorrectxx##
## Chi-squared test for given probabilities
##
## data: benford.df4$Häufigkeiten
## X-squared = 0.0014013, df = 8, p-value = 1Computer-generierte Zufallszahlen und das NBL
Wir wollen nun ein paar Zufallszahlen erzeugen um zu sehen, ob diese auch dem NBL entsprechen. Wir erzeugen dazu 10000 gleichverteilte Zufallszahlen im Bereich von 0 bis 1, multiplizieren diese mit einer zufälligen Ganzzahl zwischen 0 und 1000 und geben die dazugehörige Häufigkeitstabelle aus:
n = 10000
m = round(runif(1, min=0, max=1000))
benford.random <- runif(n, min=0, max=1) * m
benford.data3 <- sapply(benford.random, firstDigit)
benford.tab3 <- prop.table(as.numeric(table(benford.data3)))
benford.df3 <- data_frame(x=1:9, y=benford.tab3*100)
colnames(benford.df3) <- c("Führende Ziffer", "Häufigkeit (Zufall)")
knitr::kable(benford.df3)| Führende Ziffer | Häufigkeit (Zufall) |
|---|---|
| 1 | 37.81 |
| 2 | 36.64 |
| 3 | 3.49 |
| 4 | 3.60 |
| 5 | 3.76 |
| 6 | 3.65 |
| 7 | 3.59 |
| 8 | 3.60 |
| 9 | 3.86 |
full_join(benford.df, benford.df3, by="Führende Ziffer") %>%
gather("Type", "Prozent", c(2,3)) %>%
ggplot(aes(x = `Führende Ziffer`, y = Prozent, fill = Type)) +
geom_col(position = position_dodge(0.9)) +
scale_x_continuous(breaks = 1:9) +
scale_fill_hue(name="Quelle", h.start = 10, direction = -1,
breaks=c("Häufigkeit (Zufall)", "Wahrscheinlichkeit"),
labels=c("Zufallszahlen", "Benford-Verteilung")) +
ggtitle("Vergleich der Benford-Verteilung mit den Zufallszahlen-Häufigkeiten")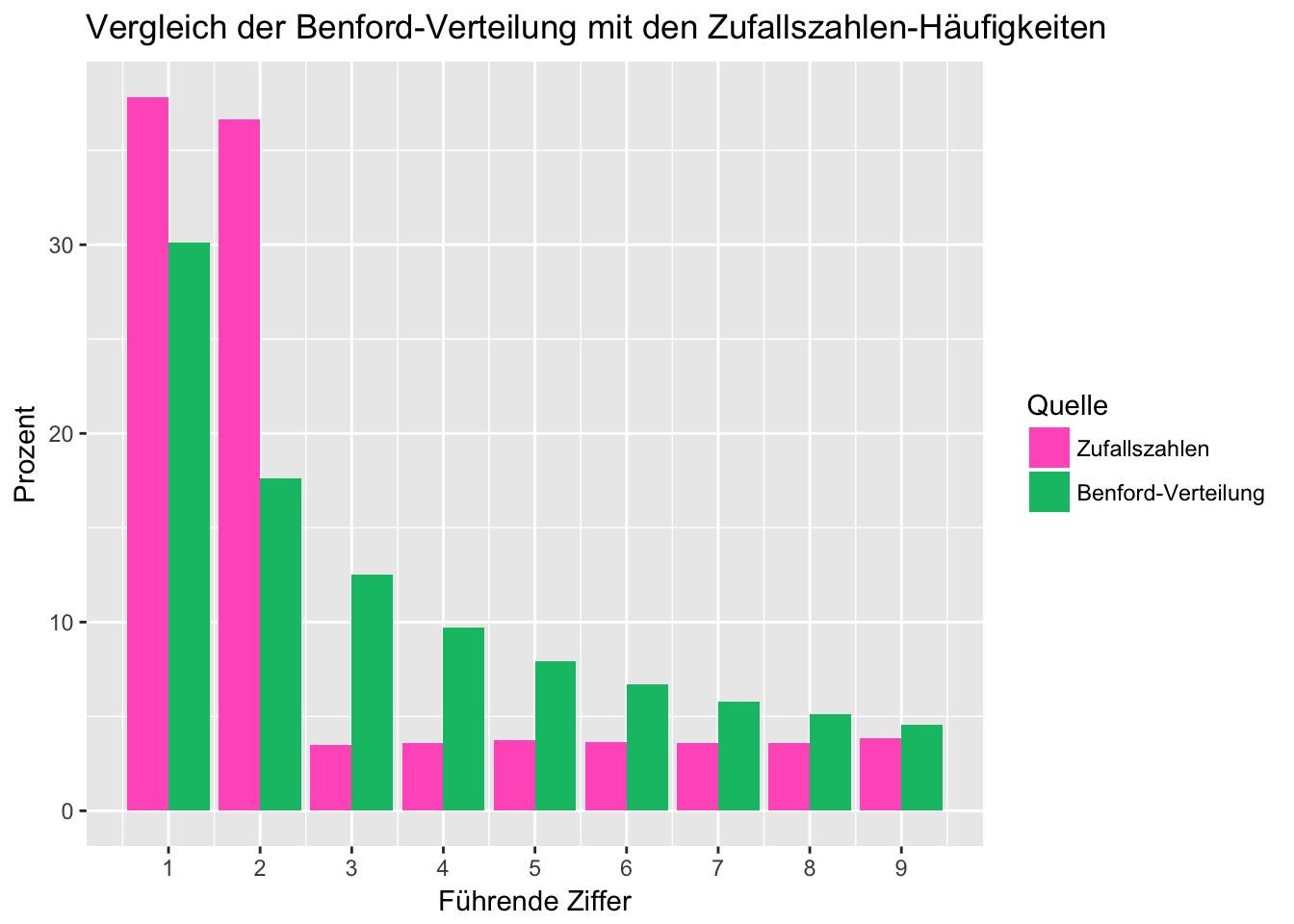
Anwendung in der Praxis
Data Scientists machen sich das Benfordsche Gesetz zu Nutze, um Auffälligkeiten in Zahlen aufzuspüren. In der Wirtschaftsprüfung und Forensik ist diese Analyse-Methode recht beliebt, um sich einen Eindruck von nummerischen Daten zu verschaffen, insbesondere von Finanztransaktionen. Die Auffälligkeit durch Abweichung vom Newcomb-Benfordchen Gesetz entsteht u.a. dadurch, dass Menschen eine unbewusste Vorliebe für bestimmte Ziffern oder Zahlen haben. Greifen Menschen in “natürliche” Daten massenhaft ein, ist es wahrscheinlich, dass sie damit auch vom Muster des Newcomb-Benfordschen Gesetzes abweichen. Weicht das Muster in Zahlungsströmen vom Newcomb-Benfordschen Erwartungsmuster für bestimmte Ziffern signifikant ab, könnte dies auf Fälle von unnatürlichen Eingriffen hindeuten.
Dieser Ansatz wird auch gerne eingesetzt, um Datenfälschungen in wissenschaftlichen Arbeiten oder Bilanzfälschungen aufzudecken. Sie ist dabei jedoch kein Beweis, sondern liefert nur die Indizien, die weitere Detailanalysen nach sich ziehen.
Nach einer Idee aus: https://data-science-blog.com/de/blog/2016/09/21/benford-analyse/
Weitere Links:
- https://www.wi.uni-muenster.de/sites/wi/files/publications/ab133.pdf
- http://www.fit-for-bit.de/Datenanalyse-mittels-Statistischer-Gesetzmaessigkeiten.php
- http://www.stochastik-in-der-schule.de/sisonline/struktur/Jahrgang29-2009/Heft3/2009-3_BradleyFarnsworth.pdf
- http://www.i-analyzer.de/resources/Benford_Betrugsaufdeckung.pdf