Cook Abstand

Vorbereitungen

Wir wollen mit mosaic arbeiten, also laden wir das Paket als erstes:

library(mosaic)

Falls die tipping-Daten noch nicht im Verzeichnis liegen, laden wir diese aus dem Internet nach:

if (!file.exists("tips.csv")) {
  download.file("https://goo.gl/whKjnl", destfile = "tips.csv")
}

Nun laden wir die tipping-Daten in den Datenrahmen tips:

tips <- read.csv2("tips.csv")

Wir brauchen für unser Modell nur den Rechnungsbetrag total_bill und den Trinkgeldbetrag tip für unser Modell:

tips %>% select(c("total_bill", "tip")) -> tips

Unser Modell:

Werfen wir zunächst einen Blick auf das Streudiagramm unserer Daten:

gf_point(tip ~ total_bill, data = tips)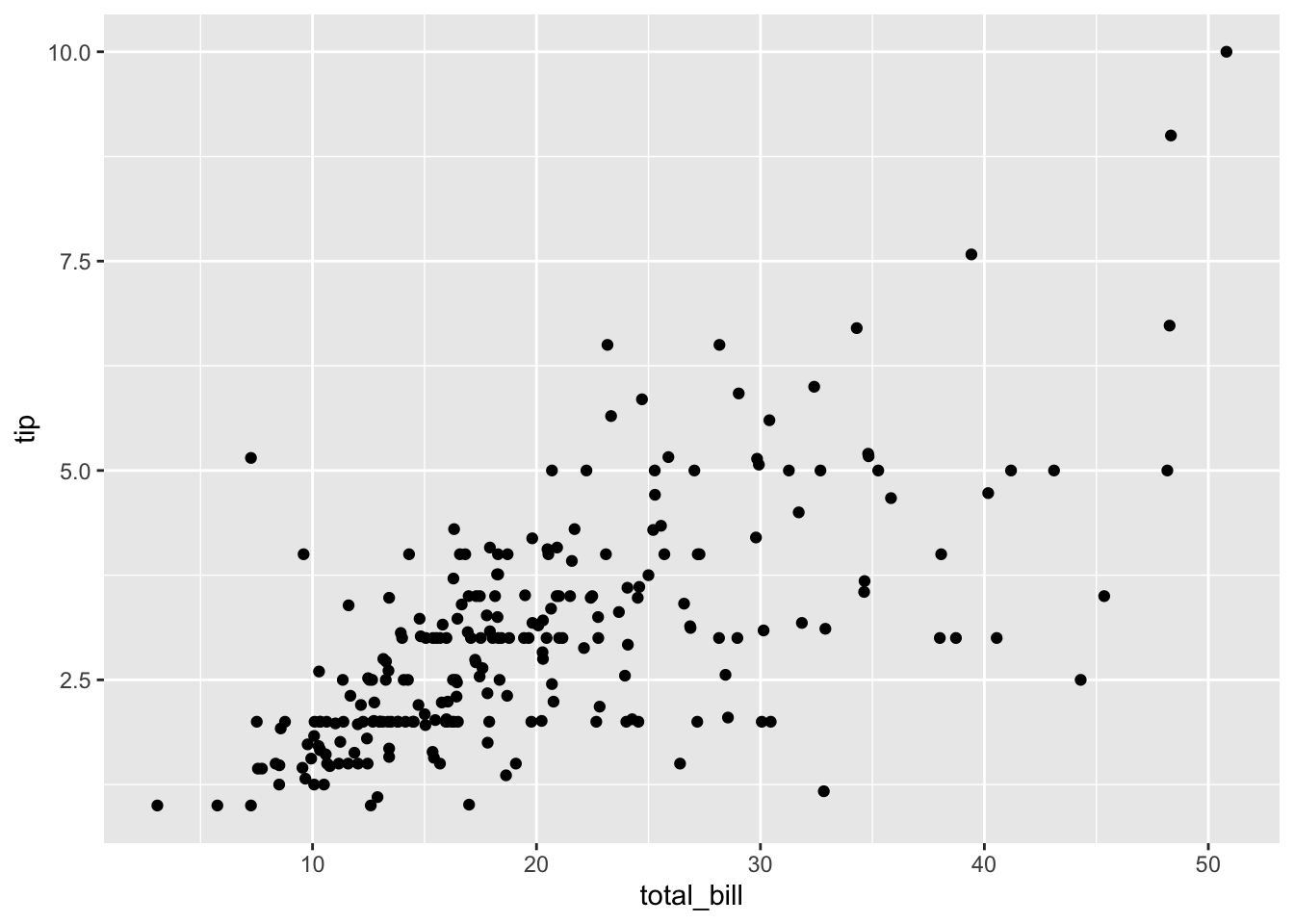

Und erstellen dann ein lineares Modell:

erg_lm <- lm(tip ~ total_bill, data = tips)
summary(erg_lm)

## 
## Call:
## lm(formula = tip ~ total_bill, data = tips)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.1982 -0.5652 -0.0974  0.4863  3.7434 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.920270   0.159735   5.761 2.53e-08 ***
## total_bill  0.105025   0.007365  14.260  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.022 on 242 degrees of freedom
## Multiple R-squared:  0.4566, Adjusted R-squared:  0.4544 
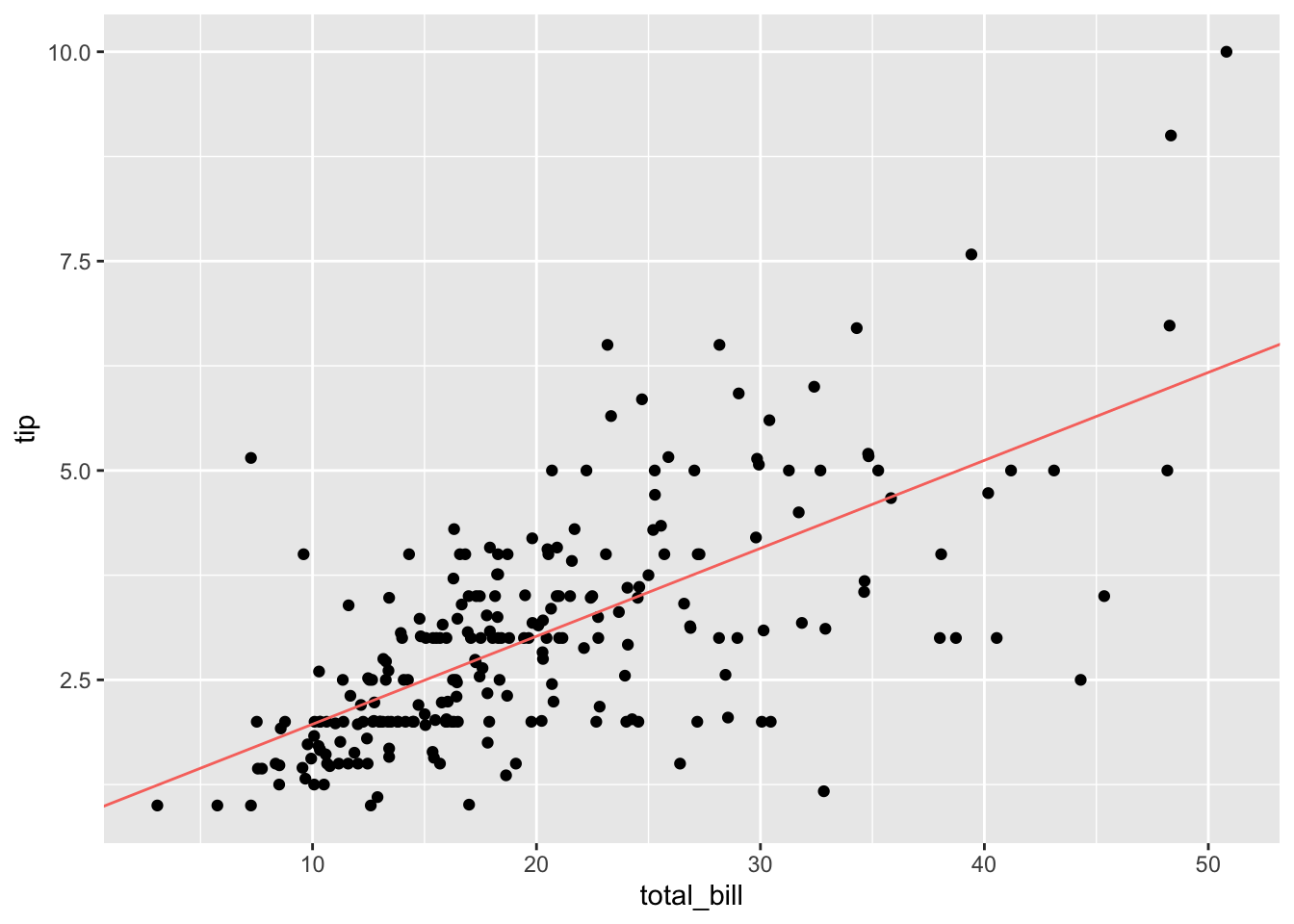
## F-statistic: 203.4 on 1 and 242 DF,  p-value: < 2.2e-16

Betrachten wir nun die Regressionsgerade in unseren Daten:

gf_point(tip ~ total_bill, data = tips) %>%
  gf_coefline(
    model = erg_lm,
    color = ~ "Regressionsgerade",
    show.legend = FALSE
  ) 

Für lineare Regressionsmodell können einflussreiche Ausreißer sehr hinderlich sein. Was ändert sich, wenn wir einen Wert, z.B. einen potentiellen Ausreißer, nicht betrachten?

Als Beispiel wählen wir die folgende Beobachtung aus:

tips %>% slice(173) -> tips_removed
tips_removed

##   total_bill  tip
## 1       7.25 5.15

tips %>% slice(-173) -> tips_red
erg_lm_red <- lm(tip ~ total_bill, data = tips_red)
summary(erg_lm_red)

## 
## Call:
## lm(formula = tip ~ total_bill, data = tips_red)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.2136 -0.5351 -0.0818  0.4951  3.6869 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.86065    0.15709   5.479 1.08e-07 ***
## total_bill   0.10731    0.00723  14.843  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9992 on 241 degrees of freedom
## Multiple R-squared:  0.4776, Adjusted R-squared:  0.4754 
## F-statistic: 220.3 on 1 and 241 DF,  p-value: < 2.2e-16

gf_point(tip ~ total_bill, data = tips_red) %>%
  gf_coefline(
    model = erg_lm,
    color = ~ "Regressionsgerade"
    ) %>%
  gf_point(
    tip ~ total_bill, 
    colour = ~ "Entfernter Punkt",
    data = tips_removed)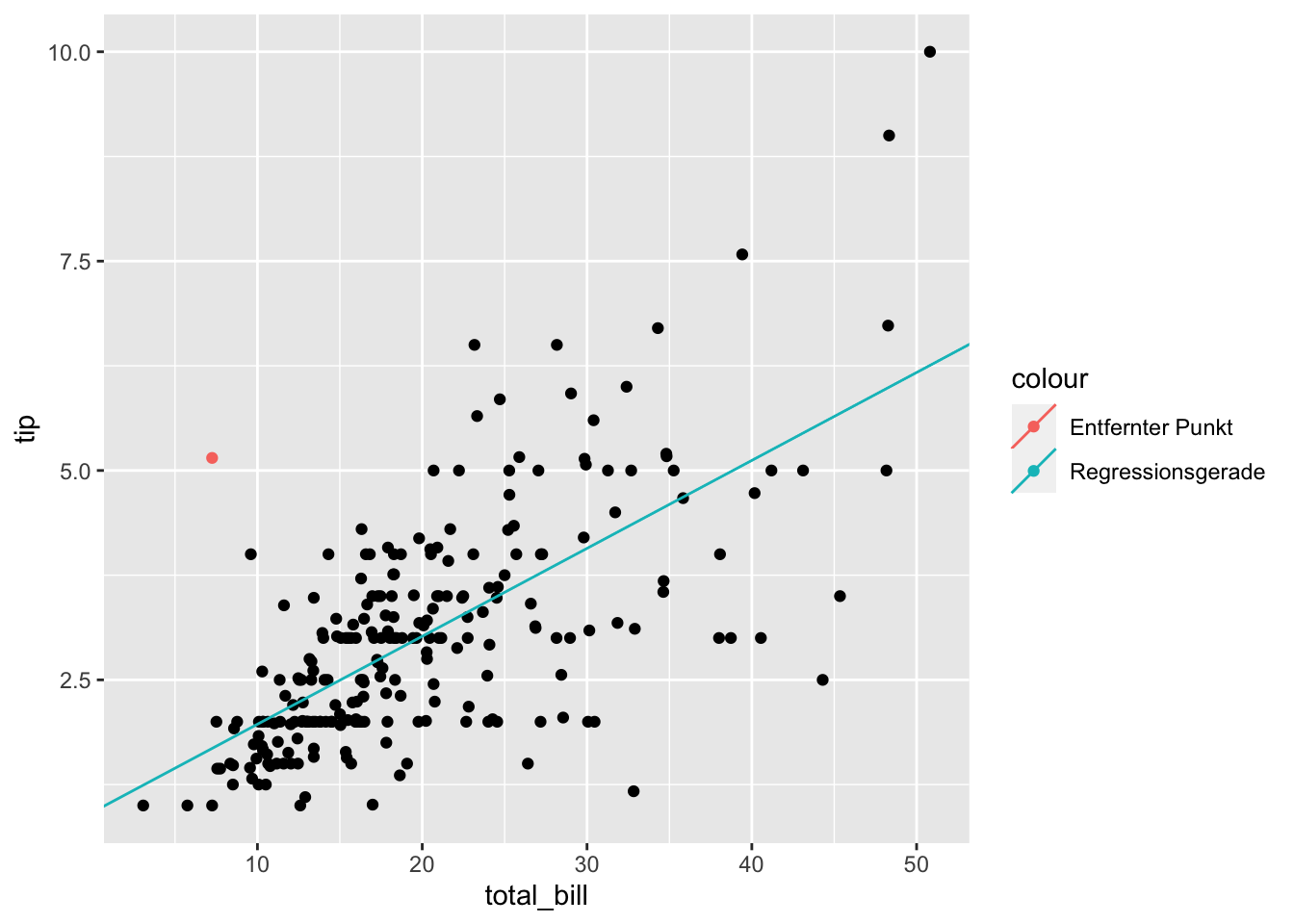

Um zu messen was diese Änderung bewirkt hat, schaut sich der Cook Abstand zunächst die Summe der quadrierten Differenzen der vorhergesagten Werte in beiden Modellen an:

new_data <- tibble(total_bill = tips$total_bill)
prognose_lm <- predict(erg_lm, newdata = new_data)
prognose_lm_red <- predict(erg_lm_red, newdata = new_data)

\[d_j = \sum_{i=1}^n \left(\hat{y}_i - \hat{y}_{i(j)}\right)^2\] Dabei ist \(\hat{y}_i\) die Prognose des Wertes \(y_i\) auf Basis von \(x_i\) mit dem Originalmodell und \(\hat{y}_{i(j)}\) die Prognose wenn man die \(j\)-te Beobachtung aus dem Modell gestrichen hat.

d_j <- sum((prognose_lm - prognose_lm_red)^2)
d_j

## [1] 0.1511406

Der Cook Abstand \(D_j\) wird nun noch normiert durch \[{\text{var}_{\text{cook}}} = p \cdot s_{\epsilon_i^2}^2\] Dabei ist \(s_{\epsilon_i^2}^2\) der erwartungstreue Schätzer der Varianz der Residuen und \(p\) die Anzahl aller erklärenden Variablen (hier \(1\)) \(+ 1\).

Es ist also:

\[D_j = \frac{d_j}{\text{var}_{\text{cook}}} = \frac{\sum\limits_{i=1}^n \left(\hat{y}_i - \hat{y}_{i(j)}\right)^2}{p \cdot s_{\epsilon_i^2}^2}\]

# Summary des Modells
selm <- summary(erg_lm)

# Wir finden p als rank im Modell
p <- erg_lm$rank 

# Wir finden den erwatungtreuen Schätzer im Summary des Modells
s_quad_eps_quad <- (selm$sigma)^2 

var_cook = p * s_quad_eps_quad

D_j = d_j / var_cook
D_j

## [1] 0.07234504

Wir können den Wert aber auch viel einfacher direkt berechnen lassen und dass für alle \(j\) mit Hilfe von cooks.distance(..):

cooks.distance(erg_lm)[173]

##        173 
## 0.07234504

Wann aber ist nun ein Wert ein einflussreicher Ausreißer?

Cook selber gibt dafür die Bedingung \(D_j > 1\) an. Andere Autor*innen schreiben \(D_j > 4/n\), wobei \(n\) die Anzahl der Beobachtung ist.

In unserem Beispiel liefert die Variante \(D_j > 1\)

cooks <- cooks.distance(erg_lm)
names(cooks) <- NULL
n <- nrow(tips)

any(cooks > 1)

## [1] FALSE

keinen Ausreißer.

Wenn wir jedoch mit \(D_j > 4/n\) suchen .

any(cooks > 4/n)

## [1] TRUE

dann gibt es Ausreißer.

Die Indices dieser finden wir mit:

which(cooks > 4/n)

##  [1]  24  48  57 103 142 157 171 173 179 183 184 185 188 208 211 213 215 238

Bereinigen wir nun unsere Daten um genau diese Werte:

remove <- which(cooks > 4/n)
tips %>% slice(-remove) -> tips_no_outliers
tips %>% slice(remove) -> tips_removed
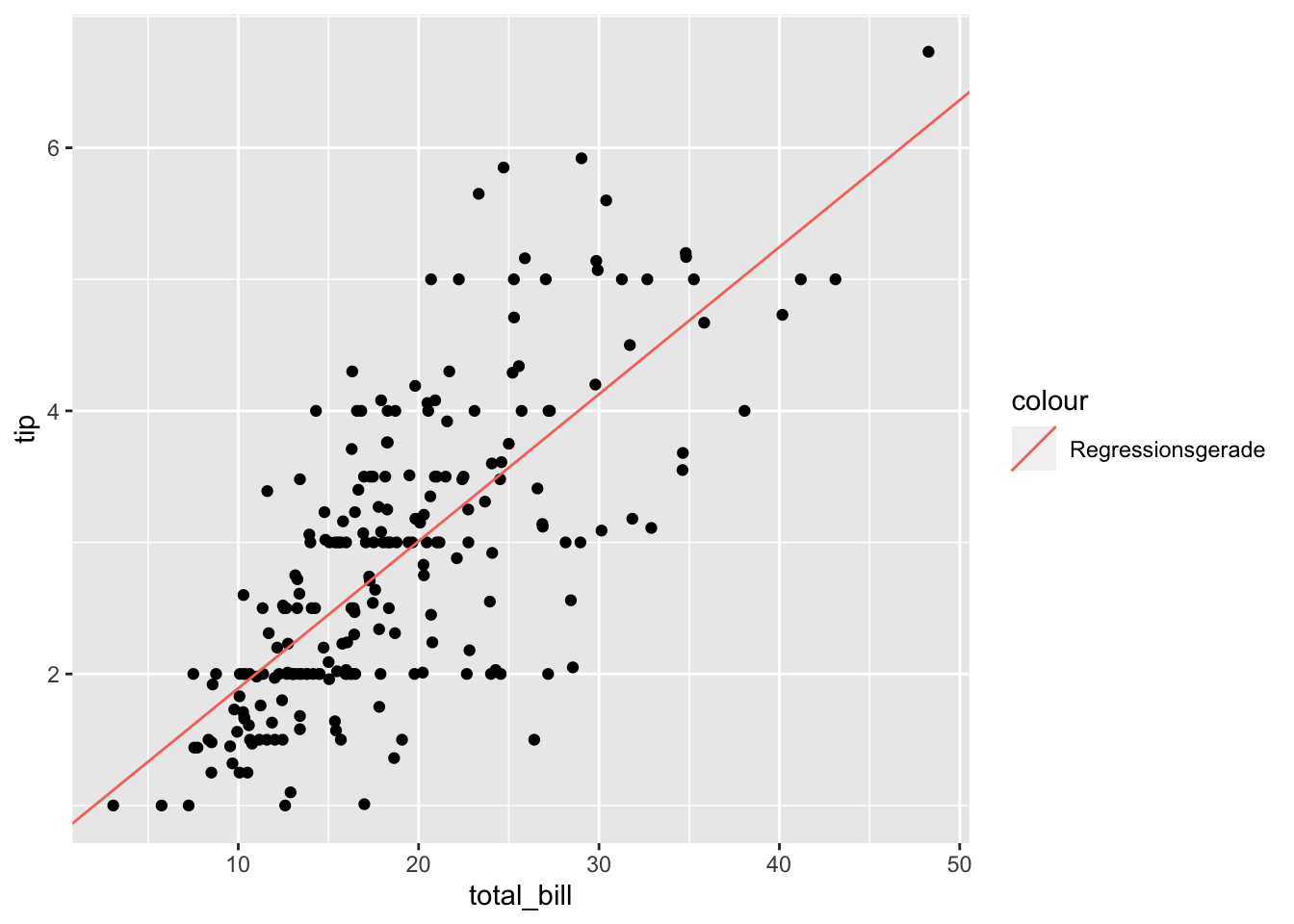
erg_lm_no_outliers <- lm(tip ~ total_bill, data = tips_no_outliers)

Und schauen uns das Ergebnis an:

summary(erg_lm_no_outliers)

## 
## Call:
## lm(formula = tip ~ total_bill, data = tips_no_outliers)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.22592 -0.48166 -0.06794  0.46992  2.31414 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.773324   0.139435   5.546  8.2e-08 ***
## total_bill  0.111799   0.006958  16.069  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7778 on 224 degrees of freedom
## Multiple R-squared:  0.5355, Adjusted R-squared:  0.5334 
## F-statistic: 258.2 on 1 and 224 DF,  p-value: < 2.2e-16

gf_point(tip ~ total_bill, data = erg_lm_no_outliers) %>%
  gf_coefline(
    model = erg_lm_no_outliers, 
    color = ~"Regressionsgerade"
  )

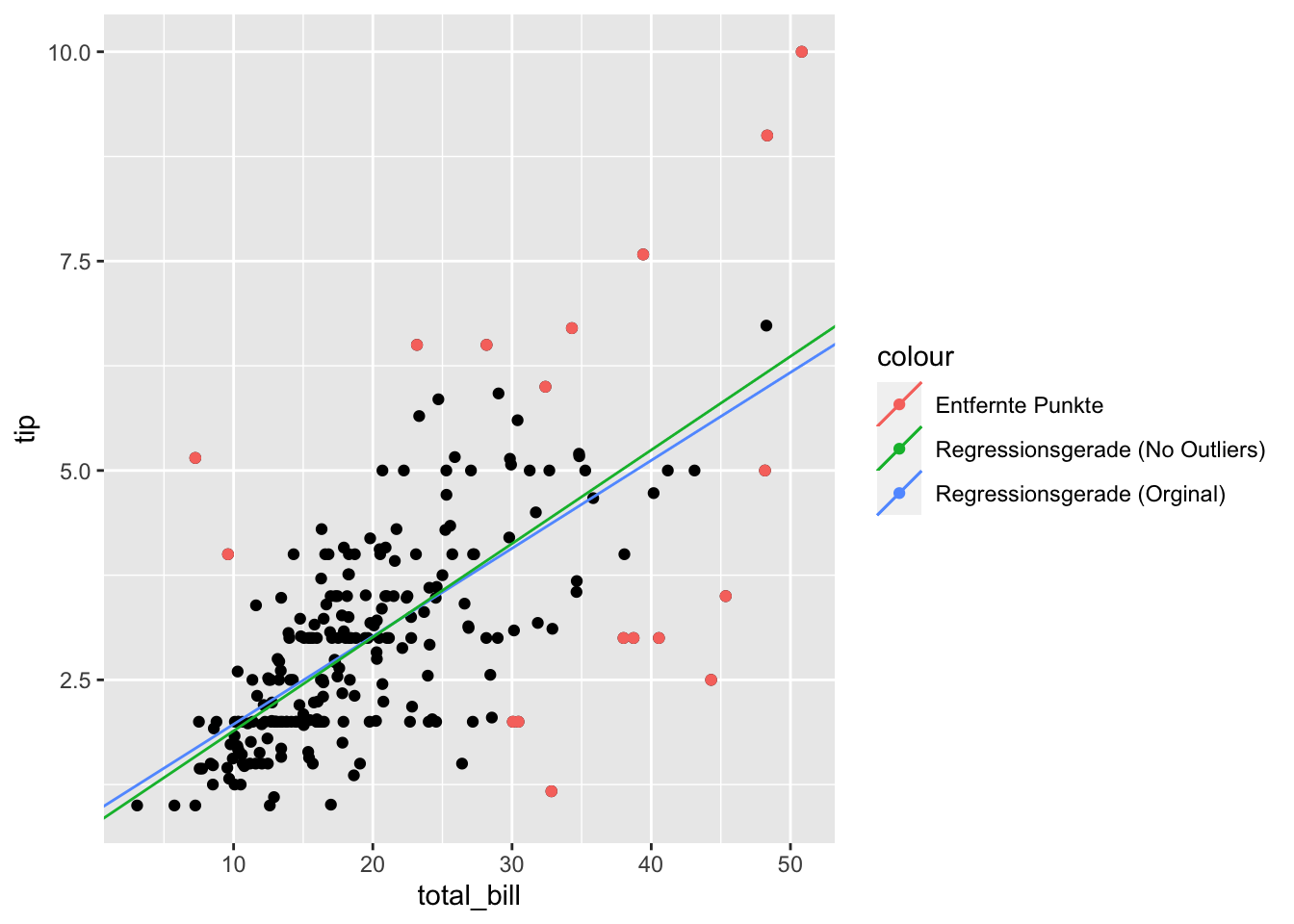
Im direkten Vergleich:

gf_point(tip ~ total_bill, data = erg_lm) %>%
  gf_coefline(
    model =  erg_lm,
    color = ~ "Regressionsgerade (Orginal)"
  ) %>%
  gf_coefline(
    model = erg_lm_no_outliers,
    color = ~ "Regressionsgerade (No Outliers)"
  ) %>%
  gf_point(
    tip ~ total_bill,
    color = ~ "Entfernte Punkte",
    data = tips_removed
  )

Unsere beiden Modelle als Formeln

Das ursprüngliche Modell: \[\widehat{tips}_{lm} = 0.9202696 + 0.1050245 \cdot total\_bill + \epsilon\]

Das um pot. Ausreißer bereinigte Modell: \[\widehat{tips}_{lm\_no} 0.7733236 + 0.1117985 \cdot total\_bill + \epsilon\]